题目内容
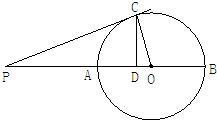 已知:如图,AB是⊙O的直径,点C是⊙O上一点,CD⊥AB,垂足为D,点P在BA的延长线上,且PC是圆O的切线.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,CD⊥AB,垂足为D,点P在BA的延长线上,且PC是圆O的切线.(1)求证:∠PCD=∠POC;
(2)若OD:DA=1:2,PA=8,求圆的半径的长.
分析:(1)根据切线的性质发现直角OCP,再根据等角的余角相等进行证明;
(2)根据OD:DA=1:2,设OD=x,DA=2x,根据直角三角形的射影定理列方程求解.
(2)根据OD:DA=1:2,设OD=x,DA=2x,根据直角三角形的射影定理列方程求解.
解答:解:(1)∵PC是圆O的切线,
∴OC⊥PC.
又CD⊥AB,
∴∠PCD=∠POC.
(2)设OD=x,DA=2x,
根据两个角对应相等得到△PCO∽△CDO,
则OC2=OD•OP,即9x2=x(8+3x),
解得x=
或x=0(不合题意,应舍去),
则圆的半径是3x=4.
∴OC⊥PC.
又CD⊥AB,
∴∠PCD=∠POC.
(2)设OD=x,DA=2x,
根据两个角对应相等得到△PCO∽△CDO,
则OC2=OD•OP,即9x2=x(8+3x),
解得x=
| 4 |
| 3 |
则圆的半径是3x=4.
点评:考查了与圆有关的比例线段、切线的性质定理和直角三角形的射影定理.属于基础题.

练习册系列答案
相关题目
 已知:如图,AB是⊙O的弦,点C在
已知:如图,AB是⊙O的弦,点C在 
 【选修4-1:几何证明选讲】
【选修4-1:几何证明选讲】 已知:如图,AB是圆C:x2+y2+4x-12y+24=0的弦,且过点P(0,5).
已知:如图,AB是圆C:x2+y2+4x-12y+24=0的弦,且过点P(0,5).