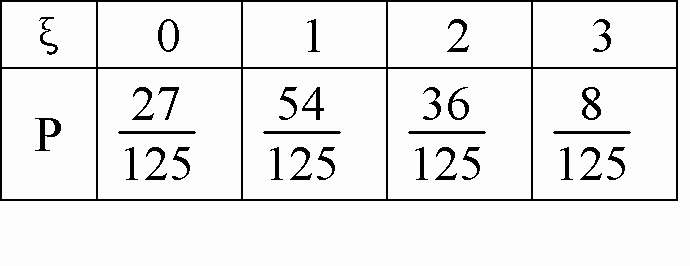题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:记"甲投篮1次投进"为事件A1,"乙投篮1次投进"为事件A2,"丙投篮1次投进"为事件A3,"3人都没有投进"为事件A.则P(A1)=,P(A2)=,P(A3)=, ∴P(A)=P()=P()·P()·P() =[1-P(A1)]·[1-P(A2)]·[1-P(A3)]=(1-)(1-)(1-)= ∴3人都没有投进的概率为 |
(2) |
解法一:随机变量ξ的可能值有0,1,2,3),ξ~B(3,), P(ξ=k)=C3k()k()3-k(k=0,1,2,3),Eξ=np=3×=. 解法二:ξ的概率分布为:
Eξ=0×+1×+2×+3×= |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
| |||||||||||