Question

【题目】某工厂生产A、B两种产品，已知制造A产品1 kg要用煤9 t，电力4 kw，劳力(按工作日计算）3个；制造B产品1 kg要用煤4 t，电力5 kw，劳力10个。又已知制成A产品1 kg可获利7万元，制成B产品1 kg可获利12万元。现在此工厂由于受到条件限制只有煤360 t，电力200 kw，劳力300个，在这种条件下应生产A、B产品各多少kg能获得最大的经济效益？

Answer 1

【答案】当生产A产品20kg、B产品24kg时，能获得最大的经济效益428万元

【解析】

试题分析：设出变量，确定不等式组，可得可行域，利用线性规划知识，可求最值

试题解析：设此工厂应分别生产A、B产品x kg，y kg，利润z万元，则

利润目标函数

作出不等式组所表示的平面区域(如图）

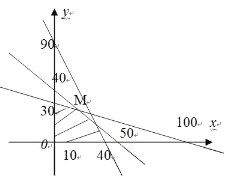
由变为，

可知当直线经过M点Z取得最大值。

由 得

答：当生产A产品20kg、B产品24kg时，能获得最大的经济效益428万元。