题目内容
(本小题满分12分)
设函数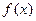 的定义域为
的定义域为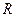 ,对任意
,对任意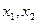 有
有
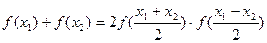 ,且
,且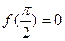 ,
,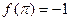 .
.
(1)求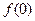 的值;
的值;
(2)求证: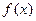 是偶函数,且
是偶函数,且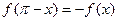 ;
;
(3)若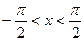 时,
时,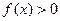 ,求证:
,求证: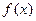 在
在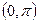 上单调递减.
上单调递减.
设函数
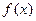 的定义域为
的定义域为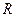 ,对任意
,对任意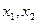 有
有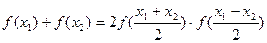 ,且
,且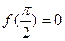 ,
,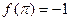 .
.(1)求
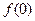 的值;
的值; (2)求证:
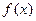 是偶函数,且
是偶函数,且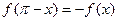 ;
; (3)若
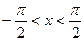 时,
时,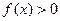 ,求证:
,求证: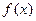 在
在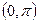 上单调递减.
上单调递减.(1)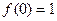
(2)略
(3)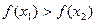 ,所以
,所以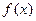 在
在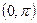 上单调递减.
上单调递减.
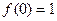
(2)略
(3)
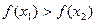 ,所以
,所以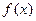 在
在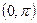 上单调递减.
上单调递减.(1)令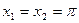 ,可得
,可得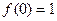 ——————4分
——————4分
(2)令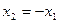 ,可得
,可得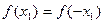 ;——————6分
;——————6分
令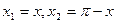 ,可得
,可得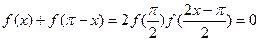 ——8分
——8分
(3)任取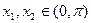 ,且
,且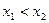 ,
,

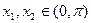 ,且
,且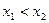 ,故
,故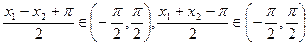
∴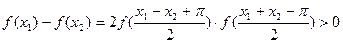
即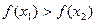 ,所以
,所以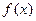 在
在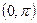 上单调递减. ————12分
上单调递减. ————12分
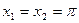 ,可得
,可得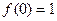 ——————4分
——————4分(2)令
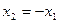 ,可得
,可得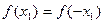 ;——————6分
;——————6分令
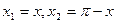 ,可得
,可得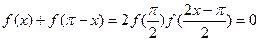 ——8分
——8分(3)任取
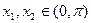 ,且
,且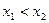 ,
,
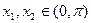 ,且
,且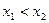 ,故
,故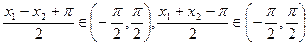
∴
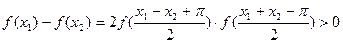
即
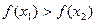 ,所以
,所以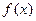 在
在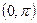 上单调递减. ————12分
上单调递减. ————12分
练习册系列答案
相关题目
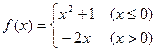
 ,若
,若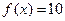 ,则
,则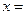

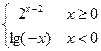 ,则 f [f (-10)] 的值为
,则 f [f (-10)] 的值为 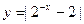 的单调增区间为
的单调增区间为  .
.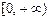 时,f (x) = x-1,则f (x-1) < 0的解集是( )
时,f (x) = x-1,则f (x-1) < 0的解集是( )
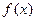 的图像是两条直线的一部份,如上图所示,其定义
的图像是两条直线的一部份,如上图所示,其定义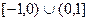 ,则不等式
,则不等式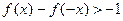 的解集为
的解集为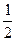 <x≤1
<x≤1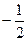 或0<x≤1
或0<x≤1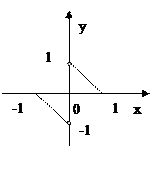
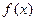 满足
满足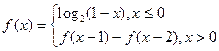 ,则
,则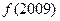 的值为 。
的值为 。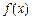 满足
满足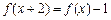 ,则
,则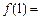 ( )
( )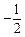 D.
D.