题目内容

已知F1、F2分别是椭圆
x2
4
+
y2
3
=1的左、右焦点，A是椭圆上一动点，圆C与F1A的延长线、F1F2的延长线以及线段AF2相切，若M（t，0）为一个切点，则（　　）
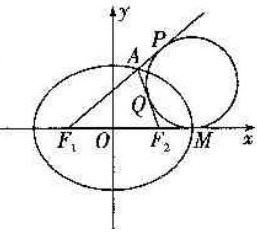
分析：由题意知，圆C是△AF1F2的旁切圆，点M是圆C与x轴的切点，设圆C与直线F1A的延长线、AF2分别相切于点P，Q，
则由切线的性质可知：AP=AQ，F2Q=F2M，F1P=F1M，由此能求出t的值．
解答：解：由题意知，圆C是△AF1F2的旁切圆，
点M是圆C与x轴的切点，
设圆C与直线F1A的延长线、AF2分别相切于点P，Q，
则由切线的性质可知：
AP=AQ，F2Q=F2M，F1P=F1M，
∴MF2=QF2=（AF1+AF2）-（AF1+AQ）
=2a-AF1-AP
=2a-F1P
=2a-F1M
∴MF1+MF2=2a，
∴t=a=2．
故选A．
点评：本题主要考查椭圆标准方程，简单几何性质，直线与椭圆的位置关系，圆的简单性质等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．
练习册系列答案
相关题目
（2013•湖南）已知F1，F2分别是椭圆E：
x25
+y2=1的左、右焦点F1，F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点．
（Ⅰ）求圆C的方程；
（Ⅱ）设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a，b．当ab最大时，求直线l的方程．
（2013•青岛二模）已知F1、F2分别是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，P为双曲线右支上的一点，
PF2
⊥
F1F2
，且|
PF1
|=
2
|
PF2
|，则双曲线的离心率为（　　）
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1 (a＞0， b＞0)的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（　　）
如图，已知F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，且椭圆C的离心率e=
1
2
，F1也是抛物线C1：y2=-4x的焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F2的直线l交椭圆C于D，E两点，且2
DF2
=
F2E
，点E关于x轴的对称点为G，求直线GD的方程．
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左，右焦点，P是双曲线的上一点，若
PF1
•
PF2
=0且|
PF1
|•|
PF2
|=3ab，则双曲线的离心率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网