题目内容
(2013•青岛二模)已知F1、F2分别是双曲线C:
-
=1(a>0,b>0)的左、右焦点,P为双曲线右支上的一点,
⊥
,且|
|=
|
|,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF2 |
| F1F2 |
| PF1 |
| 2 |
| PF2 |
分析:由于|PF1|=
|PF2|故点P是靠近F2的那一支上的一点则可根据双曲线的定义可得|PF1|-|PF2|=2a再结合|PF1|=
|PF2|求出|PF1|,|PF2|的值然后再根据PF1⊥PF2可|PF1|2-|PF2|2=|F1F2|2即可得出关于a,c的关系式从而可求出离心率e=
.
| 2 |
| 2 |
| c |
| a |
解答:解:∵|PF1|=
|PF2|
∴|PF1|-|PF2|=2a
∴|PF1|=2a(2+
),|PF2|=2a(1+
)
∵PF1⊥PF2,|F1F2|=2c
∴|PF1|2-|PF2|2=|F1F2|2
∴c2=(3+2
)a2
∴e=
=1+
故答案为:1+
.
| 2 |
∴|PF1|-|PF2|=2a
∴|PF1|=2a(2+
| 2 |
| 2 |
∵PF1⊥PF2,|F1F2|=2c
∴|PF1|2-|PF2|2=|F1F2|2
∴c2=(3+2
| 2 |
∴e=
| c |
| a |
| 2 |
故答案为:1+
| 2 |
点评:本题主要考查了双曲线的离心率的求解,属中档题,较难.解题的关键是抓住要求离心率即根据题中条件建立关于a,b,c的关系式!

练习册系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=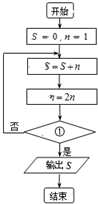 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )