Question

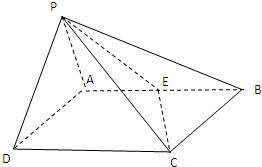在四棱锥P-ABCD中，底面ABCD是矩形，AD=2，侧面PAD是正三角形且与底面ABCD垂直，E是AB中点，PC与平面ABCD所成角为30？．
（1）证明：CD⊥平面PAD；
（2）求二面角P-CE-D的大小；
（3）求点D到平面PCE的距离．

Answer 1

分析：（1）取AD中点O，可以得出PO⊥面ABCD，∠PCO=30°，以O为原点，OD所在直线为x轴，建立空间直角坐标系，通过得出

CD • OP =0 CD • OD =0

证出

CD ⊥ OP CD ⊥ OD

后，可以证出CD⊥平面PAD
（2）分别求出平面PCE、平面DEC的一个法向量，利用两法向量的夹角求出二面角P-CE-D的大小
（3）点D到平面PCE的距离等于

CD

在

n

方向上的投影的绝对值．

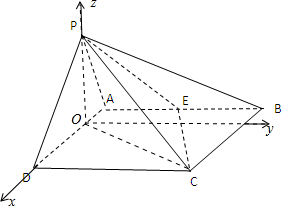解答：解
（1）证明：取AD中点O．连接OP，∵△PAD为等边三角形，
∴PO⊥AD，又面PAD⊥面ABCD，∴PO⊥面ABCD，连接OC，则
∠PCO为PC与平面ABCD所成角，∠PCO=30°．AD=2，则OP=

3

．OC=3，
∴DC=2

2

．以O为原点，OD所在直线为x轴，建立空间直角坐标系．则O（0，0，0）
D（1，0，0），P（0，0，

3

），C（1，2

2

，0），E（-1，

2

，0）
∴

OD

=（1，0，0），

OP

=（0，0，

，3

），

CD

=（0，-2

2

，0），得出

CD • OP =0 CD • OD =0

∴

CD ⊥ OP CD ⊥ OD

又OD∩OP=O，
∴CD⊥平面PAD；
（2）由（1）得

PE

=（-1，

2

，-

3

），

PC

=（1，2

2

，-

3

）
设平面PCE的一个法向量为

n

=（x，y，z），则

n • PE =0 n • PC =0

即

-x+ 2 y- 3 z=0 x+2 2 y- 3 z=0

取 x=1，则得为

n

=（1，-

2

，-

3

），又易知平面DEC的一个法向量为

OP

=（0，0，

3

）
∴cos＜

OP，

n

＞=

OP • n

| OP| • | n |

=-

2

2

．因为二面角P-CE-D是锐二面角，所以二面角P-CE-D的大小是45°．
（3）

CD

=（0，-2

2

，0），由（2）知平面PCE的一个法向量为

n

=（1，-

2

，-

3

），

CD

在

n

方向上的投影为

CD • n

| n |

=

4

6

=

2 6

3

，
∴点D到平面PCE的距离为

2 6

3

．

点评：本题考查直线和平面垂直的判定，二面角、点面距的计算．利用空间向量的方法，思路相对固定，能降低思维难度，正确的应用计算公式是关键，易错点是有时不能够准确写出相关点和向量的坐标．