题目内容
称一个函数是“好函数”当且仅当其满足:(1)定义在R上;(2)存在a<b,使其在(-∞,a),(b,+∞)上单调递增,在(a,b)上单调递减,则以下函数是好函数的有
①y=|x-2|;
②y=x|x-2|;
③y=x3-3x+1;
④y=x3+x+3.
②③
②③
(填写函数编号)①y=|x-2|;
②y=x|x-2|;
③y=x3-3x+1;
④y=x3+x+3.
分析:①和②可讨论x去绝对值,然后根据二次函数可得函数的单调区间,③和④都是多项式函数,可利用导数研究函数的单调区间,然后根据“好函数”的定义进行判定即可.
解答:解:①中函数y=|x-2|定义域为R,y=|x-2|=
∴不存在a,使y=|x-2|在(-∞,a)上单调递增,故不正确;
②中函数y=x|x-2|定义域为R,y=x|x-2|=
∴y=x|x-2|在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减,满足好函数的定义,故正确;
③中函数y=x3-x+1定义域为R,则y′=3x2-1<0解得x∈(-
,
),
y′=3x2-1>0解得x∈(-∞,-
)∪(
,+∞),
∴y=x3-x+1在(-∞,-
)、(
,+∞)上单调递增,在(-
,
)上单调递减,满足好函数的定义,故正确;
④中函数y=x3+x+3定义域为R,则y′=3x2+1>0恒成立
故不存在a<b,使函数y=x3+x+3在(a,b)上单调递减,不满足好函数的定义,故不正确;
故答案为:②③
|
∴不存在a,使y=|x-2|在(-∞,a)上单调递增,故不正确;
②中函数y=x|x-2|定义域为R,y=x|x-2|=
|
∴y=x|x-2|在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减,满足好函数的定义,故正确;
③中函数y=x3-x+1定义域为R,则y′=3x2-1<0解得x∈(-
| ||
| 3 |
| ||
| 3 |
y′=3x2-1>0解得x∈(-∞,-
| ||
| 3 |
| ||
| 3 |
∴y=x3-x+1在(-∞,-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
④中函数y=x3+x+3定义域为R,则y′=3x2+1>0恒成立
故不存在a<b,使函数y=x3+x+3在(a,b)上单调递减,不满足好函数的定义,故不正确;
故答案为:②③
点评:本题主要考查了利用导数研究函数的单调性,以及绝对值函数的处理方法和新定义,同时考查了转化的思想,属于中档题.

练习册系列答案
相关题目
 定义在
定义在 上;
上; 存在
存在 ,使其在
,使其在 上单调递增,在
上单调递增,在 上单调递减,则以下函数是“好函数”的有 .
上单调递减,则以下函数是“好函数”的有 . ;?
;? ;?
;? ;④
;④
 上;(2)存在
上;(2)存在 ,使其在
,使其在 、
、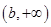 上单调递增,在
上单调递增,在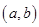 上单调递减.则以下函数中不是好函数的是
上单调递减.则以下函数中不是好函数的是







 8
8