题目内容
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°2AC=AA1=BC=2。
(Ⅰ)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(Ⅱ)若二面角B1-DC-C1的大小为60°,求AD 的长。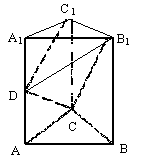
(Ⅰ)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(Ⅱ)若二面角B1-DC-C1的大小为60°,求AD 的长。

(2)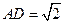
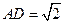
(1)证明:如图,以C为原点,CA、CB、CC1所在直线为x,y,z轴建立空间直角坐标系,则C(0,0,0),A(1,0,0),B1(0,2,2),

C1(0,0,2),D(1,0,1)。
即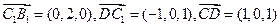 ,由
,由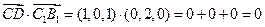 ,得
,得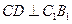 ;由
;由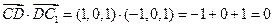 ,得
,得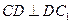 ;
;
又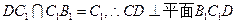 。又
。又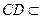 平面
平面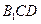 ,∴平面B1CD⊥平面B1C1D。
,∴平面B1CD⊥平面B1C1D。
(2)设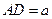 ,则D点坐标为
,则D点坐标为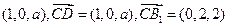 ,设平面B1CD的法向量为
,设平面B1CD的法向量为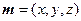 。则由
。则由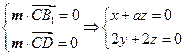 ,令
,令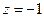 ,得
,得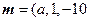 ,又平面C1DC的法向量为
,又平面C1DC的法向量为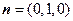 ,则
,则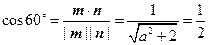 ,
,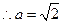 ,故
,故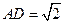 。………………12分
。………………12分

C1(0,0,2),D(1,0,1)。
即
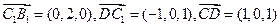 ,由
,由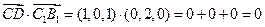 ,得
,得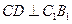 ;由
;由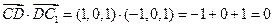 ,得
,得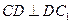 ;
;又
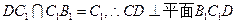 。又
。又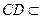 平面
平面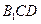 ,∴平面B1CD⊥平面B1C1D。
,∴平面B1CD⊥平面B1C1D。(2)设
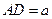 ,则D点坐标为
,则D点坐标为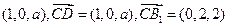 ,设平面B1CD的法向量为
,设平面B1CD的法向量为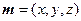 。则由
。则由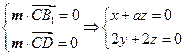 ,令
,令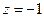 ,得
,得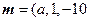 ,又平面C1DC的法向量为
,又平面C1DC的法向量为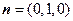 ,则
,则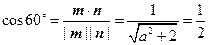 ,
,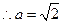 ,故
,故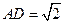 。………………12分
。………………12分
练习册系列答案
相关题目

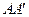 与
与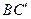 所成的角为
所成的角为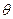 ,求
,求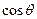 .
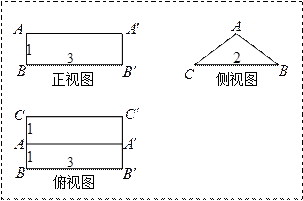
.
 倍
倍 倍
倍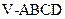 中,
中,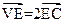 ,则三棱锥
,则三棱锥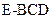 与几何体VABED的体积之比为 ( )
与几何体VABED的体积之比为 ( )