题目内容
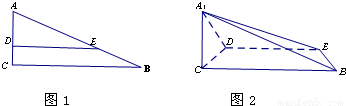
如图,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.(1)求证:A1C⊥平面BCDE;
(2)过点E作截面EFH∥平面A1CD,分别交CB于F,A1B于H,求截面EFH的面积;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE成60的角?说明理由.
【答案】分析:(1)证明DE⊥平面A1CD,可得A1C⊥DE,利用A1C⊥CD,CD∩DE=D,即可证明A1C⊥平面BCDE;
(2)过点E作EF∥CD交BC于F,过点F作FH∥A1C交A1B于H,连结EH,则截面EFH∥平面A1CD,从而可求截面EFH的面积;
(3)假设线段BC上存在点P,使平面A1DP与平面A1BE成60°的角,建立坐标系,利用向量知识,结合向量的夹角公式,即可求出结论.
解答:(1)证明:∵CD⊥DE,A1D⊥DE,CD∩A1D=D,
∴DE⊥平面A1CD.
又∵A1C?平面A1CD,∴A1C⊥DE.
又A1C⊥CD,CD∩DE=D,
∴A1C⊥平面BCDE…(4分)
(2)解:过点E作EF∥CD交BC于F,过点F作FH∥A1C交A1B于H,连结EH,则截面EFH∥平面A1CD.
因为四边形EFCD为矩形,所以EF=CD=1,CF=DE=4,从而FB=2,HF=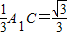 .
.
∵A1C⊥平面BCDE,FH∥A1C,
∴HF⊥平面BCDE,∴HF⊥FE,
∴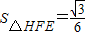 .…(8分)
.…(8分)
(3)解:假设线段BC上存在点P,使平面A1DP与平面A1BE成60°的角.
设P点坐标为(a,0,0),则a∈[0,6].
如图建系C-xyz,则D(0,1,0),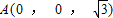 ,B(6,0,0),E(4,1,0).
,B(6,0,0),E(4,1,0).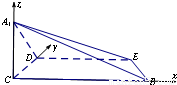
∴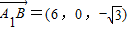 ,
,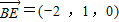 .
.
设平面A1BE法向量为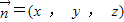 ,
,
则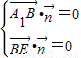 ,
,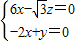 ∴
∴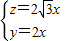 ,∴
,∴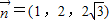 ,
,
设平面A1DP法向量为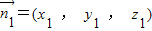 ,因为
,因为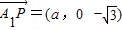 ,
,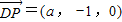 .
.
则 ,∴
,∴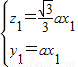 ,∴
,∴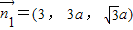 .
.
则 ,∴5656a2-96a-141=0,
,∴5656a2-96a-141=0,
解得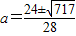
∵0<a<,6∴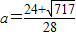
所以存在线段BC上存在点P,使平面A1DP与平面A1BE成60°的角.…(12分)
点评:本题考查线面平行,考查线面角,考查学生分析解决问题的能力,属于中档题.
(2)过点E作EF∥CD交BC于F,过点F作FH∥A1C交A1B于H,连结EH,则截面EFH∥平面A1CD,从而可求截面EFH的面积;
(3)假设线段BC上存在点P,使平面A1DP与平面A1BE成60°的角,建立坐标系,利用向量知识,结合向量的夹角公式,即可求出结论.
解答:(1)证明:∵CD⊥DE,A1D⊥DE,CD∩A1D=D,
∴DE⊥平面A1CD.
又∵A1C?平面A1CD,∴A1C⊥DE.
又A1C⊥CD,CD∩DE=D,
∴A1C⊥平面BCDE…(4分)
(2)解:过点E作EF∥CD交BC于F,过点F作FH∥A1C交A1B于H,连结EH,则截面EFH∥平面A1CD.
因为四边形EFCD为矩形,所以EF=CD=1,CF=DE=4,从而FB=2,HF=
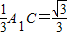 .
.∵A1C⊥平面BCDE,FH∥A1C,
∴HF⊥平面BCDE,∴HF⊥FE,
∴
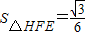 .…(8分)
.…(8分)(3)解:假设线段BC上存在点P,使平面A1DP与平面A1BE成60°的角.
设P点坐标为(a,0,0),则a∈[0,6].
如图建系C-xyz,则D(0,1,0),
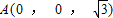 ,B(6,0,0),E(4,1,0).
,B(6,0,0),E(4,1,0).
∴
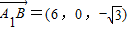 ,
,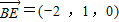 .
.设平面A1BE法向量为
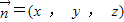 ,
,则
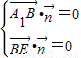 ,
,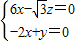 ∴
∴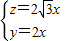 ,∴
,∴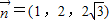 ,
,设平面A1DP法向量为
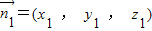 ,因为
,因为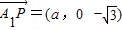 ,
,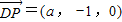 .
.则
 ,∴
,∴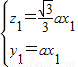 ,∴
,∴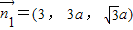 .
.则
 ,∴5656a2-96a-141=0,
,∴5656a2-96a-141=0,解得
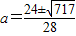
∵0<a<,6∴
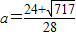
所以存在线段BC上存在点P,使平面A1DP与平面A1BE成60°的角.…(12分)
点评:本题考查线面平行,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=