题目内容
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
分析:由已知条件推导出,AD=CD=BD=
,BC=x,取BC中点E,翻折前DE=
AC=
,翻折后AE=
,AD=
,从而求出0<x<
.翻折后,当△B1CD与△ACD在一个平面上,∠A=60°,BC=ACtan60°,此时x=1×
=
,由此能求出x的取值范围为(0,
].
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:由题意得,AD=CD=BD=
,BC=x,取BC中点E,
翻折前,在图1中,连接DE,CD,则DE=
AC=
,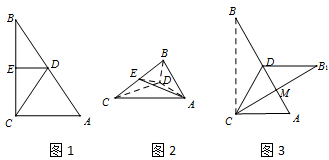
翻折后,在图2中,此时 CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴AE=
,AD=
,
在△ADE中:①
+
>
,②
<
+
,③x>0;
由①②③可得0<x<
.
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时x=1×
=
综上,x的取值范围为(0,
],
故选:A.
| ||
| 2 |
翻折前,在图1中,连接DE,CD,则DE=
| 1 |
| 2 |
| 1 |
| 2 |

翻折后,在图2中,此时 CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴AE=
1-
|
| ||
| 2 |
在△ADE中:①
| ||
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
| 1 |
| 2 |
1-
|
由①②③可得0<x<
| 3 |
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时x=1×
| 3 |
| 3 |
综上,x的取值范围为(0,
| 3 |
故选:A.
点评:本题考查线段长的取值范围的求法,要熟练掌握翻折问题的性质,注意培养空间思维能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=