题目内容
(本小题满分16分)设数列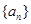 的前n项和为
的前n项和为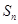 ,已知
,已知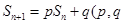 为常数,
为常数,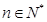 ),eg
),eg 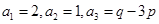
(1)求p,q的值;
(2)求数列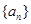 的通项公式;
的通项公式;
(3)是否存在正整数m,n,使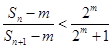 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
【答案】
⑴由题意,知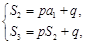 即
即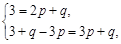 解之得
解之得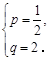 …………… 4分
…………… 4分
⑵由⑴知,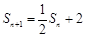 ,①
,①
当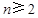 时,
时,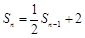 ,②
,②
①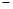 ②得,
②得,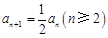 ,…………………………………………………… 6分
,…………………………………………………… 6分
又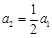 ,所以
,所以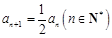 ,所以
,所以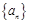 是首项为
是首项为 ,公比为
,公比为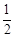 的等比数列,
的等比数列,
所以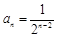 .…………………………………………………………………… 8分
.…………………………………………………………………… 8分
⑶由⑵得,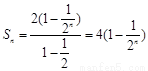 ,由
,由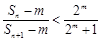 ,得
,得
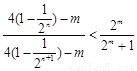 ,即
,即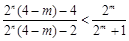 ,……………………… 10分
,……………………… 10分
即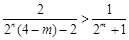 ,因为
,因为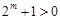 ,所以
,所以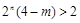 ,
,
所以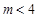 ,且
,且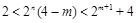 ,
,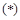
因为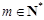 ,所以
,所以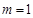 或
或 或
或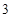 .……………………………………………… 12分
.……………………………………………… 12分
当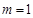 时,由
时,由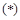 得,
得,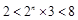 ,所以
,所以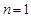 ;
;
当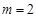 时,由
时,由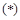 得,
得,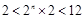 ,所以
,所以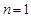 或
或 ;
;
当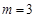 时,由
时,由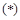 得,
得,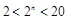 ,所以
,所以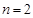 或
或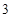 或
或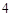 ,
,
综上可知,存在符合条件的所有有序实数对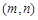 为:
为:
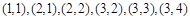 .…………………………………………… 16分
.…………………………………………… 16分
【解析】略

练习册系列答案
相关题目
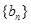 满足
满足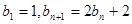 ,
,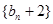 为等比数列 (2)求数列
为等比数列 (2)求数列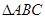 外接圆的半径为2,
外接圆的半径为2,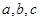 分别是
分别是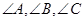 的对边
的对边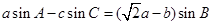
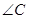 (2)求
(2)求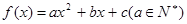 ,若不等式
,若不等式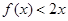 的解集为
的解集为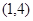 ,且方程
,且方程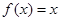 有两个相等的实数根.(1)求
有两个相等的实数根.(1)求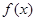 的解析式;(2)若不等式
的解析式;(2)若不等式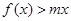 在
在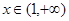 上恒成立,求实数
上恒成立,求实数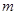 的取值范围;
的取值范围; 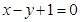 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为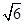
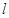 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线