题目内容
(本小题满分16分)
已知二次函数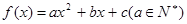 ,若不等式
,若不等式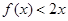 的解集为
的解集为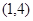 ,且方程
,且方程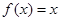 有两个相等的实数根.(1)求
有两个相等的实数根.(1)求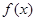 的解析式;(2)若不等式
的解析式;(2)若不等式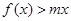 在
在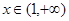 上恒成立,求实数
上恒成立,求实数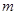 的取值范围;
的取值范围;
【答案】
(1)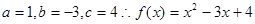 ;
;
(2) 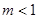 。
。
【解析】
试题分析:(1)由不等式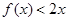 的解集为
的解集为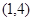 ,可知
,可知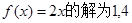 ,再根据
,再根据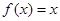 有两个相等的实数根,
有两个相等的实数根,
利用韦达定理及判别式可建立关于a,b的三个方程,还要注意a取正整数.
从而得到a,b,c的值.
(2)由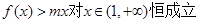 ,然后分离常数可转化为
,然后分离常数可转化为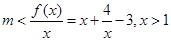 恒成立,从而转化为求
恒成立,从而转化为求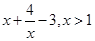 的最值,再利用基本不等式求解即可.
的最值,再利用基本不等式求解即可.
(1)由题意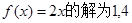 ..........3分
..........3分
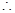
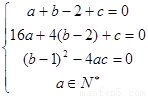 .............6分
.............6分
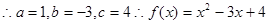 ....8分
....8分
(2)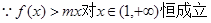
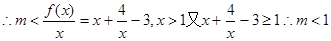 ......16分
......16分
考点:三个“二次”之间的关系,不等式恒成立问题,基本不等式求最偷.
点评:解本小题的关键是根据一元二次不等式的解集得到对应方程的根,从而得到a,b,c的值.对于不等式恒成立问题,在变量与参数能分离的情况下,转化为函数最值来研究.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足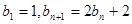 ,
,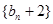 为等比数列 (2)求数列
为等比数列 (2)求数列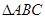 外接圆的半径为2,
外接圆的半径为2,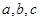 分别是
分别是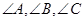 的对边
的对边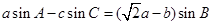
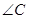 (2)求
(2)求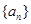 的前n项和为
的前n项和为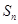 ,已知
,已知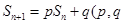 为常数,
为常数,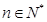 ),eg
),eg 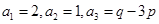
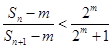 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。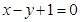 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为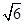
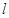 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线