题目内容
(本题满分10分)设命题p:实数x满足x2-4ax+3a2<0,其中a>0,
命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)非p是非q的充分不必要条件,求实数a的取值范围.
【答案】
(1)(2,3).(2)实数a的取值范围是(1,2].
【解析】本试题主要是考查了命题的真值,以及复合命题的真值判定,和充分条件和必要条件的判定的综合运用。
(1)先分别分析各个命题的真值为真的x的范围,然后利用交集为真,说明都是成立的x的范围可得。
(2)非p是非q的充分不必要条件利用等价命题可知q是p的充分不必要条件
说明前者的集合小于后者的集合,利用集合的包含关系解得。
解:(1)由x2-4ax+3a2<0得
(x-3a)(x-a)<0.
又a>0,所以a<x<3a,
当a=1时,1<x<3,
即p为真命题时,实数x的取值范围是1<x<3.
由
解得即2<x≤3.
所以q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则⇔2<x<3,
所以实数x的取值范围是(2,3).
(2)非p是非q的充分不必要条件,
即非p⇒非p且非q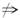 非q.
非q.
设A={x|x≤a或x≥3a},B={x|x≤2或x>3},
则A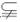 B.
B.
所以0<a≤2且3a>3,即1<a≤2.
所以实数a的取值范围是(1,2].

练习册系列答案
相关题目
 ,
,
 在
在 处与直线
处与直线 相切;
相切; 的值;②求函数
的值;②求函数 上的最大值;
上的最大值; 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. .
. ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。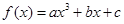
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且 ,
, 。
。 时,求
时,求 的值.
的值. 的值.
的值.