题目内容
设Tn为数列{an}的前n项之积,满足Tn=1-an(n∈N*).(1)设
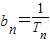 ,证明数列{bn}是等差数列,并求bn和an;
,证明数列{bn}是等差数列,并求bn和an;(2)设Sn=T12+T22+…+Tn2求证:an+1-
 <Sn≤an-
<Sn≤an- .
.
【答案】分析:(1)首先利用数列{an}的前n项积Tn与通项之间的关系分类讨论写出相邻项满足的关系式,然后两式作商,再利用 ,利用作差法即可获得数列{bn}是等差数列.由此可以求的数列{bn}的通项公式,进而求得Tn然后求得数列{an}的通项公式;
,利用作差法即可获得数列{bn}是等差数列.由此可以求的数列{bn}的通项公式,进而求得Tn然后求得数列{an}的通项公式;
(2)Sn=T12+T22+…+Tn2=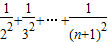 ,再进行放缩可证.
,再进行放缩可证.
解答:解:(1)∵Tn=1-an(n∈N*).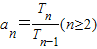 ,∴
,∴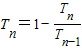 ,∴
,∴
∵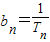 ,∴bn-bn-1=1,∵Tn=1-an,∴
,∴bn-bn-1=1,∵Tn=1-an,∴ ,∴
,∴ ,∴数列{bn}是以2为首项,以1为公差的等差数列,∴bn=n+1,∴
,∴数列{bn}是以2为首项,以1为公差的等差数列,∴bn=n+1,∴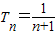 ,∴
,∴
(2)Sn=T12+T22+…+Tn2=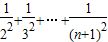

∴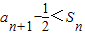
当n≥2时,=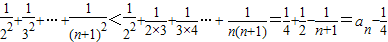
当n=1时,
∴Sn≤an- ,∴an+1-
,∴an+1- <Sn≤an-
<Sn≤an- .
.
点评:本题考查的是数列与不等式的综合类问题.在解答的过程当中充分体现了构造思想、放缩法解决不等式的证问题.
 ,利用作差法即可获得数列{bn}是等差数列.由此可以求的数列{bn}的通项公式,进而求得Tn然后求得数列{an}的通项公式;
,利用作差法即可获得数列{bn}是等差数列.由此可以求的数列{bn}的通项公式,进而求得Tn然后求得数列{an}的通项公式;(2)Sn=T12+T22+…+Tn2=
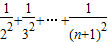 ,再进行放缩可证.
,再进行放缩可证.解答:解:(1)∵Tn=1-an(n∈N*).
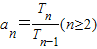 ,∴
,∴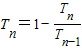 ,∴
,∴
∵
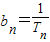 ,∴bn-bn-1=1,∵Tn=1-an,∴
,∴bn-bn-1=1,∵Tn=1-an,∴ ,∴
,∴ ,∴数列{bn}是以2为首项,以1为公差的等差数列,∴bn=n+1,∴
,∴数列{bn}是以2为首项,以1为公差的等差数列,∴bn=n+1,∴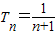 ,∴
,∴
(2)Sn=T12+T22+…+Tn2=
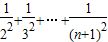

∴
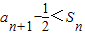
当n≥2时,=
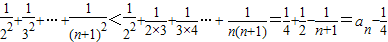
当n=1时,

∴Sn≤an-
 ,∴an+1-
,∴an+1- <Sn≤an-
<Sn≤an- .
.点评:本题考查的是数列与不等式的综合类问题.在解答的过程当中充分体现了构造思想、放缩法解决不等式的证问题.

练习册系列答案
相关题目