题目内容
已知函数f(x)=2-( sinx-cosx)2.
sinx-cosx)2.
(Ⅰ)求f( )的值和f(x)的最小正周期;
)的值和f(x)的最小正周期;
(Ⅱ)求函数在区间[- ,
, ]上的最大值和最小值.
]上的最大值和最小值.
解:(I)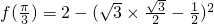 =2-1=1.
=2-1=1.
∵函数f(x)=2-( sinx-cosx)2
sinx-cosx)2
=2-
=2-(1+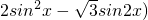
=1-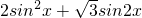
=cos2x+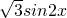
=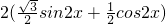
=
∴函数f(x)的周期为 .
.
(II)当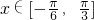 时,
时, ,
,
所以当 时,函数取得最小值
时,函数取得最小值 ;
;
当 时,函数取得最大值
时,函数取得最大值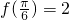 .
.
分析:(I)利用特殊角的三角函数值即可得到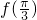 ,利用倍角公式和两角和差的正弦公式和周期公式即可得出;
,利用倍角公式和两角和差的正弦公式和周期公式即可得出;
(II)由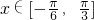 时,得到
时,得到 ,再利用正弦函数的单调性即可得到最值.
,再利用正弦函数的单调性即可得到最值.
点评:熟练掌握特殊角的三角函数值、倍角公式和两角和差的正弦公式和周期公式、正弦函数的单调性是解题的关键.
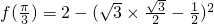 =2-1=1.
=2-1=1.∵函数f(x)=2-(
 sinx-cosx)2
sinx-cosx)2=2-

=2-(1+
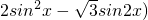
=1-
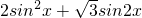
=cos2x+
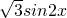
=
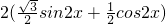
=

∴函数f(x)的周期为
 .
.(II)当
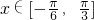 时,
时, ,
,所以当
 时,函数取得最小值
时,函数取得最小值 ;
;当
 时,函数取得最大值
时,函数取得最大值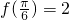 .
.分析:(I)利用特殊角的三角函数值即可得到
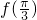 ,利用倍角公式和两角和差的正弦公式和周期公式即可得出;
,利用倍角公式和两角和差的正弦公式和周期公式即可得出;(II)由
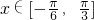 时,得到
时,得到 ,再利用正弦函数的单调性即可得到最值.
,再利用正弦函数的单调性即可得到最值.点评:熟练掌握特殊角的三角函数值、倍角公式和两角和差的正弦公式和周期公式、正弦函数的单调性是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目