题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数f(x)的单调递增区间;
,求函数f(x)的单调递增区间;
(2)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,值域为
时,值域为![]() ;当
;当![]() 时,值域为
时,值域为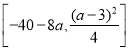 ;当
;当![]() 时,值域为
时,值域为![]() .
.
【解析】
(1)根据自变量范围化简函数,画出函数图像,根据图像得到单调区间.
(2)根据自变量范围化简函数,讨论![]() ,
,![]() ,
,![]() 三种情况,根据单调性计算最值,再讨论
三种情况,根据单调性计算最值,再讨论![]() 和
和![]() 的大小关系得到答案.
的大小关系得到答案.
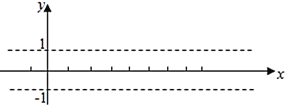
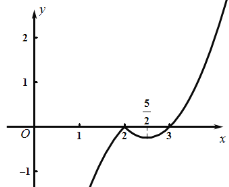
(1)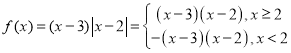 ,画出函数图像,如图所示:
,画出函数图像,如图所示:
根据图像知函数的单调增区间为![]() 和
和![]() .
.
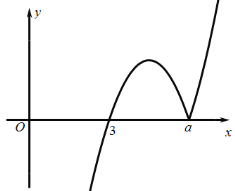
(2)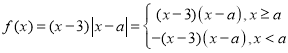 ,
,
画出函数简图,如图所示:当![]() 时,二次函数对称轴为
时,二次函数对称轴为![]() ,
,
当![]() ,即
,即![]() 时,函数在
时,函数在![]() 上单调递增,
上单调递增,
故![]() ,
,
![]() ,故值域为
,故值域为![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() ,
,
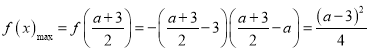 ,值域为
,值域为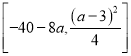 ;
;
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,取
,取![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
故当![]() 时,
时,![]() ,值域为
,值域为![]() ;
;
当![]() 时,
时,![]() ,值域为
,值域为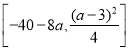 .
.
综上所述:当![]() 时,值域为
时,值域为![]() ;当
;当![]() 时,值域为
时,值域为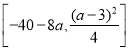 ;当
;当![]() 时,值域为
时,值域为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目