题目内容
有4名同学参加唱歌、跳舞、下棋三项比赛,每项比赛至少有1人参加,每名同学只参加一项比赛,另外甲同学不能参加跳舞比赛,则不同的参赛方案的种数为_____(用数字作答).
24
试题分析:因为将4名学生参加三项比赛,那么每项比赛至少有1人参加,则将4=1+1+2,同时由于甲同学不能参加跳舞比赛,因此可以分为两类,参加跳舞的只有一个人时,那么先选出一个人
 ,然后将其与的三个人分组为3=1+2,所有的情况有
,然后将其与的三个人分组为3=1+2,所有的情况有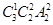 ,利用分步乘法计数原理得到为
,利用分步乘法计数原理得到为
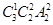 =18种,同时参加跳舞的有两个人时,则有
=18种,同时参加跳舞的有两个人时,则有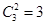 ,剩余的参加的比赛分组分配有
,剩余的参加的比赛分组分配有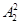 ,利用乘法计数原理可知共有
,利用乘法计数原理可知共有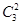
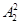 =6,结合分类计数加法原理得到为18+6=24,因此填写24.
=6,结合分类计数加法原理得到为18+6=24,因此填写24.点评:解决该试题的关键是利用已知的条件,能合理的运用分组的思想来分配人员,同时能对于特殊元素优先考虑的思想来解答,属于中档题。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
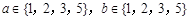 ,则方程
,则方程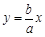 表示不同的直线有__________条.
表示不同的直线有__________条.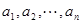 是1,2,…,
是1,2,…,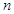 的一个排列,把排在
的一个排列,把排在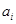 的左边且比
的左边且比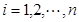 )。如:在排列
)。如:在排列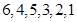 中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )
中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )