题目内容
若函数f(x)同时满足下列三个性质:①偶函数;②在区间(0,1)上是增函数;③有最小值,则y=f(x)的解析式可以是( )A.y=ex+e-x
B.y=1-x2
C.y=sin
D.
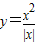
【答案】分析:由于函数 y=ex+e-x 满足①偶函数,由它的导数大于零可得满足②,利用基本不等式可以求得它的最小值,故满足①②③.再根据y=1-x2 不满足②,由于函数y=sinx
不满足①,y=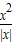 不满足③,从而得出结论.
不满足③,从而得出结论.
解答:解:由于函数 y=ex+e-x 满足①偶函数.y′=ex-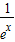 在区间(0,1)上大于零,故满足②在区间(0,1)上是增函数.
在区间(0,1)上大于零,故满足②在区间(0,1)上是增函数.
利用基本不等式可以求得它的最小值等于2,故满足③有最小值.
由于函数y=1-x2 在区间(0,1)上是减函数,故不满足②.
由于函数y=sinx是奇函数,故不满足①.
由于函数y=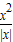 没有最小值,故不满足③,
没有最小值,故不满足③,
故选A.
点评:本题主要考查函数的奇偶性、单调性、值域,属于基础题.
不满足①,y=
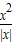 不满足③,从而得出结论.
不满足③,从而得出结论.解答:解:由于函数 y=ex+e-x 满足①偶函数.y′=ex-
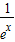 在区间(0,1)上大于零,故满足②在区间(0,1)上是增函数.
在区间(0,1)上大于零,故满足②在区间(0,1)上是增函数.利用基本不等式可以求得它的最小值等于2,故满足③有最小值.
由于函数y=1-x2 在区间(0,1)上是减函数,故不满足②.
由于函数y=sinx是奇函数,故不满足①.
由于函数y=
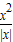 没有最小值,故不满足③,
没有最小值,故不满足③,故选A.
点评:本题主要考查函数的奇偶性、单调性、值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数f(x)同时满足①有反函数;②是奇函数;③定义域与值域相同.则f(x)的解析式可能是( )
| A、f(x)=-x3 | ||
| B、f(x)=x3+1 | ||
C、f(x)=
| ||
D、f(x)=lg
|