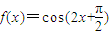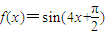题目内容
若函数f(x)同时具有以下两个性质:①f(x)是偶函数;②对任意实数x,都有f(-x+| π |
| 4 |
| π |
| 4 |
①f(x)=cos4x;
②f(x)=sin(2x+
| π |
| 2 |
③f(x)=sin(4x+
| π |
| 2 |
④f(x)=cos(
| 3π |
| 2 |
分析:根据条件先判断函数的一条对称轴是x=
,再利用诱导公式对选项中解析式进行化简,根据正弦(余弦)函数的奇偶性和对称轴方程进行逐一判断.
| π |
| 4 |
解答:解:由题意知,函数的一条对称轴是x=
,
①、f(x)=cos4x是偶函数,把x=
代入得,4x=π,则x=
是函数的对称轴,故①符合条件;
②、f(x)=sin(2x+
)=cos2x是偶函数,把x=
代入得,2x=
,则x=
不是函数的对称轴,故②不符合题意;
③、f(x)=sin(4x+
)=cos4x,同①分析,故③符合题意;
④、f(x)=cos(
-4x)=-sin4x是奇函数,故④不符合题意.
故答案为:①③.
| π |
| 4 |
①、f(x)=cos4x是偶函数,把x=
| π |
| 4 |
| π |
| 4 |
②、f(x)=sin(2x+
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
③、f(x)=sin(4x+
| π |
| 2 |
④、f(x)=cos(
| 3π |
| 2 |
故答案为:①③.
点评:本题考查了正弦(余弦)函数的奇偶性和对称性的应用,需要先通过诱导公式进行化简,考查了分析问题和解决问题的能力.

练习册系列答案
相关题目
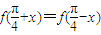 ,则f(x)的解析式可以是( )
,则f(x)的解析式可以是( )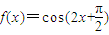
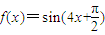
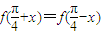 ,则f(x)的解析式可以是( )
,则f(x)的解析式可以是( )