题目内容
设F1,F2分别是椭圆D: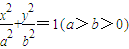 的左、右焦点,过F2作倾斜角为
的左、右焦点,过F2作倾斜角为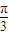 的直线交椭圆D于A,B两点,F1到直线AB的距离为3,连接椭圆D的四个顶点得到的菱形面积为4.
的直线交椭圆D于A,B两点,F1到直线AB的距离为3,连接椭圆D的四个顶点得到的菱形面积为4.(Ⅰ)求椭圆D的方程;
(Ⅱ)过椭圆D的左顶点P作直线l1交椭圆D于另一点Q.
(ⅰ)若点N(0,t)是线段PQ垂直平分线上的一点,且满足
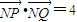 ,求实数t的值;
,求实数t的值;(ⅱ)过P作垂直于l1的直线l2交椭圆D于另一点G,当直线l1的斜率变化时,直线GQ是否过x轴上的一定点,若过定点,请给出证明,并求出该定点坐标;若不过定点,请说明理由.
【答案】分析:(Ⅰ)设出AB的方程,利用F1到直线AB的距离为3,可求得c的值,利用a2-b2=c2=3,连接椭圆D的四个顶点得到的菱形面积为4,即可求得椭圆D的方程;
(Ⅱ)设直线l1的方程代入椭圆D的方程,消去y,整理得一元二次方程,由韦达定理,可求得线段PQ的中点坐标;(ⅰ)当k=0时,则有Q(2,0),线段PQ垂直平分线为y轴,利用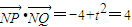 ,可求t的值;当k≠0时,求出线段PQ垂直平分线的方程,令x=0,得:
,可求t的值;当k≠0时,求出线段PQ垂直平分线的方程,令x=0,得: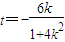 ,利用
,利用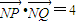 ,可求t的值;
,可求t的值;
(ⅱ)设直线l2的方程与椭圆方程联立,确定Q的坐标,从而可求GQ的直线方程,令y=0,即可得到结论.
解答:解:(Ⅰ)设F1,F2的坐标分别为(-c,0),(c,0),其中c>0
由题意得AB的方程为: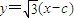
因F1到直线AB的距离为3,所以有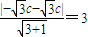 ,解得
,解得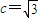 …(1分)
…(1分)
所以有a2-b2=c2=3…①
由题意知: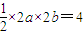 ,即ab=2…②
,即ab=2…②
联立①②解得:a=2,b=1
∴所求椭圆D的方程为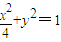 …(4分)
…(4分)
(Ⅱ)由(Ⅰ)知:P(-2,0),设Q(x1,y1)
根据题意可知直线l1的斜率存在,可设直线斜率为k,则直线l1的方程为y=k(x+2)
把它代入椭圆D的方程,消去y,整理得:(1+4k2)x2+16k2x+(16k2-4)=0
由韦达定理得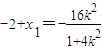 ,则
,则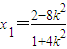 ,
,
∴y1=k(x1+2)=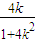 ,∴
,∴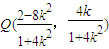 ,
,
∴线段PQ的中点坐标为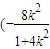 ,
,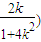 …(6分)
…(6分)
(ⅰ)当k=0时,则有Q(2,0),线段PQ垂直平分线为y轴,于是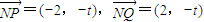
由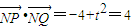 ,解得:
,解得: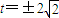 …(8分)
…(8分)
当k≠0时,则线段PQ垂直平分线的方程为y-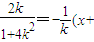
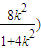
因为点N(0,t)是线段PQ垂直平分线的一点,
令x=0,得: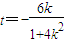 ,于是
,于是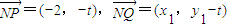
由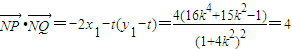 ,解得:
,解得: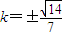
代入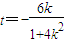 ,解得:
,解得: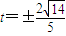
综上,满足条件的实数t的值为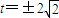 或
或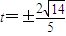 …(10分)
…(10分)
(ⅱ)设G(x2,y2),由题意知l1的斜率k≠0,直线l2的斜率为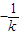 ,则
,则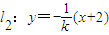
由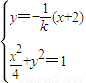 化简得:(k2+4)x2+16x+16-4k2=0.
化简得:(k2+4)x2+16x+16-4k2=0.
∵此方程有一根为-2,得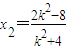 ⇒
⇒ .…(12分)
.…(12分)
∵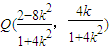 ,则
,则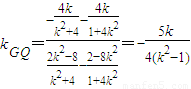
所以GQ的直线方程为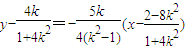
令y=0,则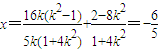 .
.
所以直线GQ过x轴上的一定点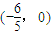 …(14分)
…(14分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,综合性强.
(Ⅱ)设直线l1的方程代入椭圆D的方程,消去y,整理得一元二次方程,由韦达定理,可求得线段PQ的中点坐标;(ⅰ)当k=0时,则有Q(2,0),线段PQ垂直平分线为y轴,利用
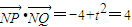 ,可求t的值;当k≠0时,求出线段PQ垂直平分线的方程,令x=0,得:
,可求t的值;当k≠0时,求出线段PQ垂直平分线的方程,令x=0,得: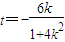 ,利用
,利用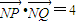 ,可求t的值;
,可求t的值;(ⅱ)设直线l2的方程与椭圆方程联立,确定Q的坐标,从而可求GQ的直线方程,令y=0,即可得到结论.
解答:解:(Ⅰ)设F1,F2的坐标分别为(-c,0),(c,0),其中c>0
由题意得AB的方程为:
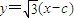
因F1到直线AB的距离为3,所以有
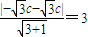 ,解得
,解得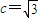 …(1分)
…(1分)所以有a2-b2=c2=3…①
由题意知:
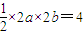 ,即ab=2…②
,即ab=2…②联立①②解得:a=2,b=1
∴所求椭圆D的方程为
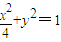 …(4分)
…(4分)(Ⅱ)由(Ⅰ)知:P(-2,0),设Q(x1,y1)
根据题意可知直线l1的斜率存在,可设直线斜率为k,则直线l1的方程为y=k(x+2)
把它代入椭圆D的方程,消去y,整理得:(1+4k2)x2+16k2x+(16k2-4)=0
由韦达定理得
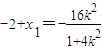 ,则
,则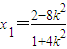 ,
,∴y1=k(x1+2)=
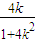 ,∴
,∴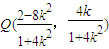 ,
,∴线段PQ的中点坐标为
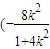 ,
,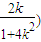 …(6分)
…(6分)(ⅰ)当k=0时,则有Q(2,0),线段PQ垂直平分线为y轴,于是
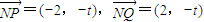
由
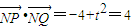 ,解得:
,解得: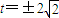 …(8分)
…(8分)当k≠0时,则线段PQ垂直平分线的方程为y-
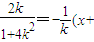
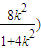
因为点N(0,t)是线段PQ垂直平分线的一点,
令x=0,得:
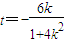 ,于是
,于是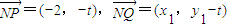
由
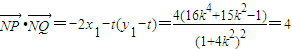 ,解得:
,解得: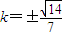
代入
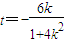 ,解得:
,解得: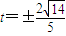
综上,满足条件的实数t的值为
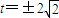 或
或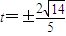 …(10分)
…(10分)(ⅱ)设G(x2,y2),由题意知l1的斜率k≠0,直线l2的斜率为
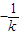 ,则
,则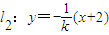
由
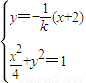 化简得:(k2+4)x2+16x+16-4k2=0.
化简得:(k2+4)x2+16x+16-4k2=0.∵此方程有一根为-2,得
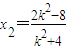 ⇒
⇒ .…(12分)
.…(12分)∵
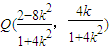 ,则
,则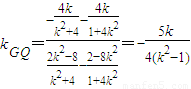
所以GQ的直线方程为
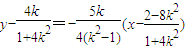
令y=0,则
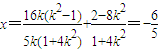 .
.所以直线GQ过x轴上的一定点
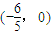 …(14分)
…(14分)点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,综合性强.

练习册系列答案
相关题目
 的左、右焦点,过F2作倾斜角为
的左、右焦点,过F2作倾斜角为 的直线交椭圆D于A,B两点,F1到直线AB的距离为3,连接椭圆D的四个顶点得到的菱形面积为4.
的直线交椭圆D于A,B两点,F1到直线AB的距离为3,连接椭圆D的四个顶点得到的菱形面积为4.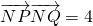 ,求实数t的值;
,求实数t的值;