题目内容
10、关于x的方程|3x-1|=k,如果它只有一个解,那么实数k 的取值范围是( )
分析:先把关于x的方程|3x-1|=k只有一个解的问题转化为函数y=|3x-1|与函数y=k的图象只有一个交点,再画出函数y=|3x-1|图象,看函数y=k的图象满足什么条件时符合要求即可求出对应实数k 的取值范围.
解答: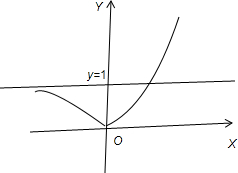 解:关于x的方程|3x-1|=k只有一个解,
解:关于x的方程|3x-1|=k只有一个解,
即是函数y=|3x-1|与函数y=k的图象只有一个交点.
画出函数y=|3x-1|图象,
由图得:
当y=k与X轴重合或满足y≥1时,两个函数的图象只有一个交点,
故所求实数k 的取值范围是k=0,k≥1.
故选 A.
 解:关于x的方程|3x-1|=k只有一个解,
解:关于x的方程|3x-1|=k只有一个解,即是函数y=|3x-1|与函数y=k的图象只有一个交点.
画出函数y=|3x-1|图象,
由图得:
当y=k与X轴重合或满足y≥1时,两个函数的图象只有一个交点,
故所求实数k 的取值范围是k=0,k≥1.
故选 A.
点评:本题主要考查根的个数问题以及转化思想和数形结合思想.数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知关于x的方程|3x-1|=k,则下列说法错误的是( )
| A、当k>1时,方程的解的个数为1个 | B、当k=0时,方程的解的个数为1个 | C、当0<k<1时,方程的解的个数为2个 | D、当k=1时,方程的解的个数为2个 |