题目内容
已经函数f(x)=2sinxcosx+sin2x-cos2x.
(1)求f(x)递增区间;
(2)求f(x)当x∈[0,
]时的值域.
(1)求f(x)递增区间;
(2)求f(x)当x∈[0,
| π |
| 2 |
∵f(x)=2sinxcosx+sin2x-cos2x
=sin2x-cos2x
=
(cos(-
)sin2x+sin(-
)cos2x)
=
sin(2x-
)
(1)f(x)递增区间为2x-
∈[-
+2kπ,
+2kπ] k∈Z
即递增区间为x∈[-
+kπ,
+kπ]k∈Z)
(2)当x∈[0,
]
即2x-
∈[-
,
]
∴f(x)min=
sin(-
)=-1
f(x)max=
sin(
)=
即f(x)当x∈[0,
]时的值域为[-1,
]
=sin2x-cos2x
=
| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 2 |
| π |
| 4 |
(1)f(x)递增区间为2x-
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
即递增区间为x∈[-
| π |
| 8 |
| 3π |
| 8 |
(2)当x∈[0,
| π |
| 2 |
即2x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴f(x)min=
| 2 |
| π |
| 4 |
f(x)max=
| 2 |
| π |
| 2 |
| 2 |
即f(x)当x∈[0,
| π |
| 2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
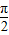 ]时的值域.
]时的值域.