题目内容
已经函数f(x)=2sinxcosx+sin2x-cos2x.
(1)求f(x)递增区间;
(2)求f(x)当x∈[0,
]时的值域.
(1)求f(x)递增区间;
(2)求f(x)当x∈[0,
| π | 2 |
分析:利用二倍角公式以及两角和与差公式化简为同角的正弦函数即可分析进行求解.
解答:解:∵f(x)=2sinxcosx+sin2x-cos2x
=sin2x-cos2x
=
(cos(-
)sin2x+sin(-
)cos2x)
=
sin(2x-
)
(1)f(x)递增区间为2x-
∈[-
+2kπ,
+2kπ] k∈Z
即递增区间为x∈[-
+kπ,
+kπ]k∈Z)
(2)当x∈[0,
]
即2x-
∈[-
,
]
∴f(x)min=
sin(-
)=-1
f(x)max=
sin(
)=
即f(x)当x∈[0,
]时的值域为[-1,
]
=sin2x-cos2x
=
| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 2 |
| π |
| 4 |
(1)f(x)递增区间为2x-
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
即递增区间为x∈[-
| π |
| 8 |
| 3π |
| 8 |
(2)当x∈[0,
| π |
| 2 |
即2x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴f(x)min=
| 2 |
| π |
| 4 |
f(x)max=
| 2 |
| π |
| 2 |
| 2 |
即f(x)当x∈[0,
| π |
| 2 |
| 2 |
点评:此题考查了二倍角公式、两角和与差公式以及同角三角函数的基本关系,熟练掌握公式是解题的关键,属于中档题.

练习册系列答案
相关题目
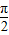 ]时的值域.
]时的值域.