题目内容
已经函数f(x)=(
)x-sinx,a∈R,则f(x)在[0,2π]上的零点个数为( )
| 1 |
| a2+2a+3 |
分析:由于a2+2a+3=(a+1)2+2≥2,可得0<
≤
.分别画出y=(
)x,y=sinx的图象.由图象可得,函数y=(
)x,y=sinx的图象交点的个数,进而得到函数f(x)零点的个数.
| 1 |
| a2+2a+3 |
| 1 |
| 2 |
| 1 |
| a2+2a+3 |
| 1 |
| a2+2a+3 |
解答:解:∵a2+2a+3=(a+1)2+2≥2,
∴0<
≤
.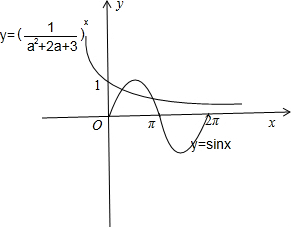
分别画出y=(
)x,y=sinx的图象.
由图象看出,函数y=(
)x,y=sinx的图象有且仅有两个交点.
因此函数f(x)=(
)x-sinx,a∈R,在[0,2π]上的零点个数为2.
故选B.
∴0<
| 1 |
| a2+2a+3 |
| 1 |
| 2 |
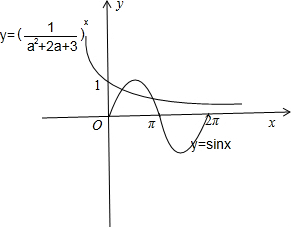
分别画出y=(
| 1 |
| a2+2a+3 |
由图象看出,函数y=(
| 1 |
| a2+2a+3 |
因此函数f(x)=(
| 1 |
| a2+2a+3 |
故选B.
点评:本题考查了指数函数与正弦函数的图象、函数零点的意义,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
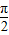 ]时的值域.
]时的值域.