��Ŀ����
����С������12�֣�
ij��ҵ����A��B���ֲ�Ʒ�������г�������Ԥ�⣬A��Ʒ��������Ͷ�ʳ����ȣ����ϵ��ͼ1��B��Ʒ��������Ͷ�ʵ�����ƽ���������ȣ����ϵ��ͼ2(ע�������Ͷ�ʵ�λ����Ԫ)��
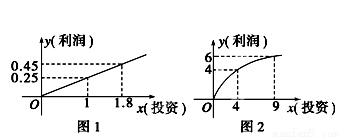
(1)�ֱ�A��B���ֲ�Ʒ�������ʾΪͶ�ʵĺ�����ϵʽ��
(2)��֪����ҵ�ѳO��18��Ԫ�ʽ𣬲���ȫ��Ͷ��A��B���ֲ�Ʒ��������
����ƽ��Ͷ���������ֲ�Ʒ���ɻ�ö�������
���ʣ�������dz���������������18��ԪͶ�ʣ�����ʹ����ҵ�������������������ԼΪ������Ԫ��
(1) f(x)��0��25x (x��0)��g(x)��2 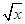 (x��0)��
(x��0)��
(2)������y��8��25(��Ԫ),��A��B���ֲ�Ʒ�ֱ�Ͷ��2��Ԫ��16��Ԫʱ����ʹ����ҵ����������8��5��Ԫ��
��������
���������(1)��ס������ֲ�Ʒ�ֱ�Ͷ��x��Ԫ(x��0)����������ֱ�Ϊf (x)��g(x)��Ԫ��
���������f(x)��k1x��g(x)��k2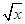 ��
��
�����ͼ��ɽ��f(x)��0��25x (x��0)��
g(x)��2 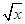 (x��0)��
(x��0)��
(2)����(1)��f(9)��2��25��g(9)��2  ��6��
��6��
��������y��8��25(��Ԫ)��
����B��ƷͶ��x��Ԫ��A��ƷͶ��(18��x)��Ԫ������ҵ�ɻ�������Ϊy��Ԫ��
��y��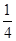 (18��x)��2
(18��x)��2 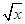 ��0��x��18��
��0��x��18��
��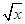 ��t��t��[0,3
��t��t��[0,3 ]��
]��
��y��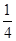 (��t2��8t��18)����
(��t2��8t��18)����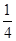 (t��4)2��
(t��4)2�� ��
��
�൱t��4ʱ��ymax�� ��8��5����ʱx��16,18��x��2��
��8��5����ʱx��16,18��x��2��
�൱A��B���ֲ�Ʒ�ֱ�Ͷ��2��Ԫ��16��Ԫʱ����ʹ����ҵ����������8��5��Ԫ��
���㣺����ģ�͵�����
���������������Ĺؼ��Ƕ�����������ʽ����⣬�ܽ�ʵ������ת��Ϊ����ʽ�������������ʣ����ڻ����⡣

 ��У����ϵ�д�
��У����ϵ�д�