题目内容
(本小题满分12分)
 某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
甲 |
11.6 |
12.2 |
13.2 |
13.9 |
14.0 |
11.5 |
13.1 |
14.5 |
11.7 |
14.3 |
|
乙 |
12.3 |
13.3 |
14.3 |
11.7 |
12.0 |
12.8 |
13.2 |
13.8 |
14.1 |
12.5 |
(I)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(Ⅲ)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
解:(Ⅰ)从统计图中可以看出,乙的成绩较为集中,差异程度较小,应选派乙同学代表班级参加比赛更好;
(Ⅱ)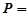
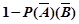 =
=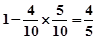 ;
;
(Ⅲ)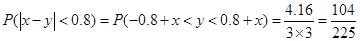 .
.
【解析】本试题主要是考查了直方图的运用,以及几何概型概率的计算和古典概型概率的综合运用。
(1)因为从统计图中可以看出,乙的成绩较为集中,差异程度较小,应选派乙同学代表班级参加比赛更好
(2)设事件A为:甲的成绩低于12.8,事件B为:乙的成绩低于12.8,
则甲、乙两人成绩至少有一个低于 秒的概率利用对立事件的概率公式可知为
秒的概率利用对立事件的概率公式可知为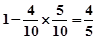
(3)设甲同学的成绩为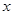 ,乙同学的成绩为
,乙同学的成绩为 ,
,
则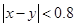 ,,那么利用几何概型概率可知结论。
,,那么利用几何概型概率可知结论。
解:(Ⅰ)
茎叶图
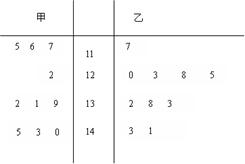
…………2分
从统计图中可以看出,乙的成绩较为集中,差异程度较小,应选派乙同学代表班级参加比赛更好;………………4分
(Ⅱ)设事件A为:甲的成绩低于12.8,事件B为:乙的成绩低于12.8,
则甲、乙两人成绩至少有一个低于 秒的概率为:
秒的概率为: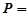
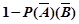 =
=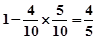 ;……………8分
;……………8分
(此部分,可根据解法给步骤分:2分)
(Ⅲ)设甲同学的成绩为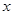 ,乙同学的成绩为
,乙同学的成绩为 ,
,
则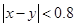 ,……………10分
,……………10分
得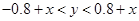 ,
,
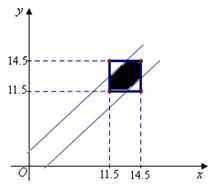
如图阴影部分面积即为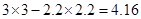 ,则
,则
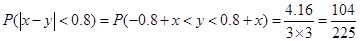 . …………12分
. …………12分

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案