题目内容
若函数y=ax与y=-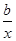 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
| A.单调递增 | B.单调递减 |
| C.先增后减 | D.先减后增 |
B
解析

练习册系列答案
相关题目
下列函数为奇函数的是( )
A.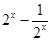 | B.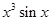 | C.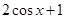 | D.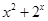 |
已知函数 是
是 上的增函数,
上的增函数, 是其图像上的两点,那么
是其图像上的两点,那么 的解集为( )
的解集为( )
A. | B. | C.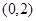 | D.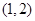 |
对任意实数 ,
, 定义运算“⊙”:
定义运算“⊙”: 设
设 ,若函数
,若函数 的图象与
的图象与 轴恰有三个交点,则
轴恰有三个交点,则 的取值范围是( )
的取值范围是( )
A.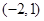 | B. |
C. | D.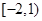 |
已知函数f(x)的图象如图所示,则f(x)的解析式可以是( )
A.f(x)= |
B.f(x)= |
C.f(x)=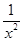 -1 -1 |
D.f(x)=x- |
已知函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+m(m为常数),则f(-1)的值为( )
| A.-3 | B.-1 | C.1 | D.3 |
已知函数g(x)=1-2x,f[g(x)]= (x≠0),则f(
(x≠0),则f( )等于( )
)等于( )
| A.1 | B.3 | C.15 | D.30 |

 的最大值为( )
的最大值为( )
| A.0 | B.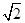 | C.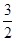 | D. |