题目内容
16.已知函数f(x)对定义域内任意x,y,有f(x+y)=f(x)+f(y).(1)求f(0);
(2)判断f(x)的奇偶性.
分析 (1)由已知中对于任意实数x,y都有f(x+y)=f(x)+f(y)成立,我们可以得到设x=y=0,则f(0)=0;
(2)再令y=-x可得f(-x)=-f(x),进而根据函数奇偶性的定义得到结论f(x)为奇函数.
解答 解:(1)令x=y=0知f(0)=0;
(2)令y=-x知f(x)+f(-x)=0,
∴f(x)为奇函数.
点评 本题考查抽象函数,考查赋值法的运用,考查学生的计算能力,比较基础.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7.函数f(x)=x+$\frac{4}{x}$的值域是( )
| A. | [4,+∞) | B. | (4,+∞) | C. | R | D. | (-∞,-4]∪[4,+∞) |
8.函数f(x)=x2+x-b2的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数 |
5.不等式2|x-5|+$\frac{2}{3}$≥$\frac{2}{3}$的解集为( )
| A. | R | B. | ($\frac{2}{3}$,+∞) | C. | ($\frac{1}{3}$,$\frac{2}{3}$) | D. | ∅ |
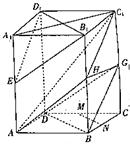 如图,在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点.
如图,在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点.