题目内容
为调查某校学生喜欢数学课的人数比例,采用如下调查方法:
(1)在该校中随机抽取 名学生,并编号
名学生,并编号 ;
;
(2)在箱内放置两个白球和三个红球,让抽取的 名学生分别从箱中随机摸出一球,记住其颜色并放回;
名学生分别从箱中随机摸出一球,记住其颜色并放回;
(3)请下列两类学生举手:(ⅰ)摸到白球且号数为偶数的学生;(ⅱ)摸到红球且不喜欢数学课的学生.
如果总共有 名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是
名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是
A. | B.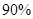 | C. | D. |
B
解析试题分析::由题意,号数为偶数的概率为 ,摸到白球的概率为
,摸到白球的概率为 =0.4,摸到红球的概率为1-0.4=0.6
=0.4,摸到红球的概率为1-0.4=0.6
那么按概率计算摸到白球且号数位偶数的学生有100× ×0.4=20个
×0.4=20个
一共有26学生举手,则有6个摸到红球且不喜欢数学课的学生,除以摸红球的概率就是不喜欢数学课的学生6÷0.6=10。那么喜欢数学课的有90个,90÷100=90%,。故选B.
考点:本题考查概率的计算。
点评:先分别计算号数为偶数的概率、摸到白球的概率、摸到红球的概率,从而可得摸到白球且号数位偶数的学生,进而可得摸到红球且不喜欢数学课的学生人数,由此可得结论。考查学生分析解决问题的能力,属于基础题.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案在建立两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数
的回归模型中,分别选择了4个不同的模型,它们的相关指数 如下,其中拟合最好的模型是( )
如下,其中拟合最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 | B.模型2的相关指数 为0.80 为0.80 |
C.模型3的相关指数 为0.50 为0.50 | D.模型4的相关指数 为0.25 为0.25 |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是
| A. x;和y正相关 |
| B. x和y的相关系数为直线l的斜率 |
| C. x和y的相关系数在-1到0之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,补全这个频率分布直方图后,估计本次考试中的平均分(统计方法中,同一组数据常用该组区间的中点值作为代表) ( )
| A.72 | B.71 | C.72.5 | D.75 |
一个社会调查机构就某地居民的月收入调查20000人,并根据所得数据画出了样本频率分布直方图,为了分析居民的收入与年龄、学历、职业等方面的关系,按月收入用分层抽样方法抽样,若从月收入 (元)段中抽取了30人,则在这20000人中共抽取的人数为( )
(元)段中抽取了30人,则在这20000人中共抽取的人数为( )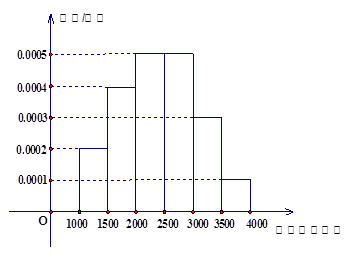
| A.200 | B.20000 | C.100 | D.40 |
为了解 1200 名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段的间隔(抽样距) 为 ( )
为 ( )
| A.40 | B.30 | C.20 | D.12 |
某商场在国庆黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为( )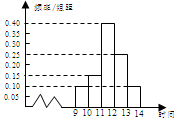
| A.6万元 | B.8万元 | C.10万元 | D.12万元 |
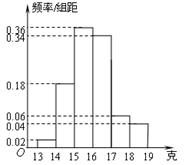
 ,净重大于等于15克且小于17克的产品数为
,净重大于等于15克且小于17克的产品数为 ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出