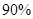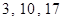题目内容
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,补全这个频率分布直方图后,估计本次考试中的平均分(统计方法中,同一组数据常用该组区间的中点值作为代表) ( )
| A.72 | B.71 | C.72.5 | D.75 |
B
解析试题分析:利用已知中给出的六段中的五段的频率值可知分数在【70,80】之间的频率为1-(0.015+0.005+0.010+0.015+0.025) 10=0.3,那么估计本次考试的平均分即为
10=0.3,那么估计本次考试的平均分即为 =71,故选B.
=71,故选B.
考点:本试题考查了直方图的运用。
点评:利用直方图求解平均值的方法就是运用各个组距之间的中点值,乘以该组的频率,然后相加得到。属于基础题。同时要通过直方图学会看众数,和中位数的值。

 阅读快车系列答案
阅读快车系列答案在刚召开的十二届全国人大一次会上,为了调查人大代表对“反腐倡廉”的意见,现从1000
名代表中使用系统抽样,按以下规定获取样本编号:如果在起始组中随机抽取的号码为M ,那么第K组(组
号K从0开始,K=0,1,2,,9)抽取的号码的百位数为组号,后两位数为M+32K的后两位数,若M=16,
则 时所抽取的样本编号为( )
时所抽取的样本编号为( )
| A.444 ,740 | B.416,716 | C.444,726 | D.423,726 |
如图是某次比赛上七位评委为某选手打出的分数的茎叶图,若去掉一个最高分和最低分,则所剩数据的平均数为 
| A.84 | B.85 | C.86 | D.87 |
、在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
 3.841时,认为两个事件无关。在一项打鼾与患心脏病的调查中,共调查了2000 人,经计算的
3.841时,认为两个事件无关。在一项打鼾与患心脏病的调查中,共调查了2000 人,经计算的 =20.87,根据这一数据分析,认为打鼾与患心脏病之间( )
=20.87,根据这一数据分析,认为打鼾与患心脏病之间( )
| A.有95%的把握认为两者有关 | B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 | D.约有99%的打鼾者患心脏病 |
要了解全市高一学生身高在某一范围的学生所占比例的大小,需知道相应样本的
| A.平均数 | B.方差 | C.众数 | D.频率分布 |
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )A、63.6万元 B、65.5万元
C、67.7万元 D、72.0万元
某实验中学共有职工150人,其中高级职称的职工15人,中级职称的职工45人,一般职员90人,现采用分层抽样抽取容量为30的样本,则抽取的高级职称、中级职称、一般职员的人数分别为
| A.5、10、15 | B.3、9、18 | C.3、10、17 | D.5、9、16 |
 名学生,并编号
名学生,并编号 ;
; 名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是
名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是