题目内容
已知数列![]()
(I)若存在一个实数![]()
(II)在(I)的条件下,求出数列![]()
解:(1)假设存在实数![]() 无关的常数。
无关的常数。

故存在实数![]() 为等差数列.
为等差数列.
(II)由(I)可得![]()
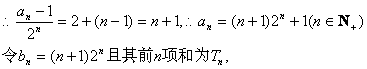
![]() ①
①
![]() ②
②
①-②得![]()
![]()
![]()

练习册系列答案
相关题目
题目内容
已知数列![]()
(I)若存在一个实数![]()
(II)在(I)的条件下,求出数列![]()
解:(1)假设存在实数![]() 无关的常数。
无关的常数。

故存在实数![]() 为等差数列.
为等差数列.
(II)由(I)可得![]()
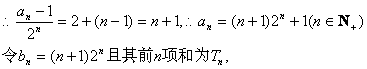
![]() ①
①
![]() ②
②
①-②得![]()
![]()
![]()
