题目内容
已知椭圆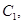 抛物线
抛物线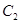 的焦点均在
的焦点均在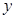 轴上,
轴上,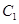 的中心和
的中心和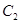 的顶点均为坐标原点
的顶点均为坐标原点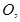 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中:
(Ⅰ)求分别适合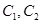 的方程的点的坐标;
的方程的点的坐标;
(Ⅱ)求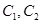 的标准方程.
的标准方程.
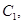 抛物线
抛物线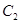 的焦点均在
的焦点均在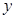 轴上,
轴上,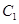 的中心和
的中心和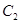 的顶点均为坐标原点
的顶点均为坐标原点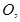 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中: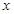 | 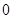 | 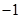 | 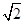 | 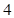 |
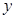 | 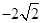 | 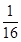 | 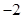 | 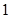 |
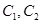 的方程的点的坐标;
的方程的点的坐标;(Ⅱ)求
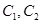 的标准方程.
的标准方程.(Ⅰ)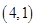 和
和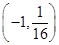 在抛物线
在抛物线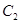 上,
上,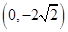 和
和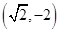 在椭圆
在椭圆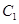 上;(Ⅱ)
上;(Ⅱ)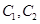 的标准方程分别为
的标准方程分别为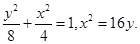 .
.
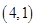 和
和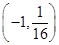 在抛物线
在抛物线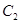 上,
上,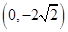 和
和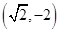 在椭圆
在椭圆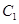 上;(Ⅱ)
上;(Ⅱ)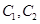 的标准方程分别为
的标准方程分别为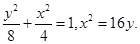 .
.试题分析:(Ⅰ)已知椭圆
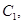 抛物线
抛物线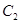 的焦点均在
的焦点均在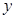 轴上,
轴上,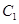 的中心和
的中心和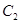 的顶点均为坐标原点
的顶点均为坐标原点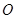 ,可设抛物线
,可设抛物线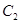 的方程为
的方程为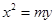 ,从每条曲线上取两个点,将其坐标记录于表中,要找出这两点,只需将这四个点都代入抛物线
,从每条曲线上取两个点,将其坐标记录于表中,要找出这两点,只需将这四个点都代入抛物线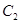 的方程,求出的
的方程,求出的 值相同两点在抛物线
值相同两点在抛物线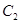 上,另外两点在椭圆上;(Ⅱ)求
上,另外两点在椭圆上;(Ⅱ)求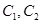 的标准方程,由(Ⅰ)的判断就求出抛物线
的标准方程,由(Ⅰ)的判断就求出抛物线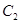 的方程,只需求椭圆的方程,由于椭圆为标准位置,且过
的方程,只需求椭圆的方程,由于椭圆为标准位置,且过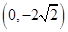 ,故
,故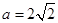 ,只需求出
,只需求出 ,又因为椭圆过
,又因为椭圆过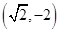 ,代入椭圆的方程可求出
,代入椭圆的方程可求出 ,从而得椭圆的方程.
,从而得椭圆的方程.试题解析:(Ⅰ)
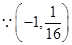 和
和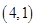 代入抛物线方程中得到的解相同,
代入抛物线方程中得到的解相同,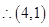 和
和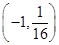 在抛物线
在抛物线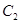 上,
上,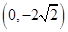 和
和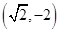 在椭圆
在椭圆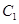 上. 4分
上. 4分(Ⅱ)设
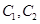 的标准方程分别为:
的标准方程分别为: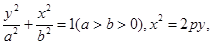
将
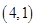 和
和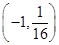 代入抛物线方程中得到的解相同,
代入抛物线方程中得到的解相同,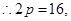 7分
7分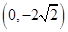 和
和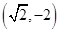 在椭圆上,代入椭圆方程得
在椭圆上,代入椭圆方程得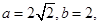 10分
10分故
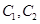 的标准方程分别为
的标准方程分别为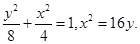 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
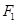 、
、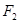 分别是椭圆
分别是椭圆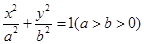 的左、右焦点,右焦点
的左、右焦点,右焦点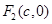 到上顶点的距离为2,若
到上顶点的距离为2,若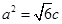 .
.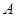 是椭圆的右顶点,直线
是椭圆的右顶点,直线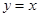 与椭圆交于
与椭圆交于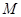 、
、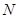 两点(
两点(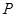 、
、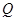 是此椭圆上两点,并且满足
是此椭圆上两点,并且满足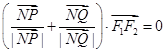 ,求证:向量
,求证:向量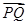 与
与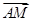 共线.
共线.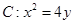 的焦点为
的焦点为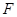 ,过点
,过点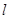 交抛物线
交抛物线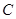 于
于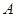 、
、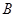 两点,经过
两点,经过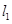 、
、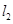 ,切线
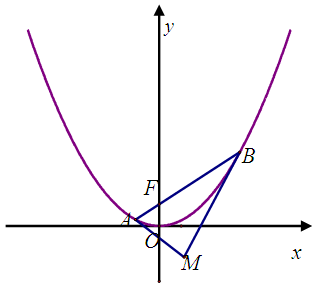
,切线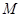 .
.
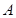 在第二象限,且到准线距离为
在第二象限,且到准线距离为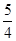 时,求
时,求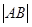 ;
;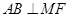 .
.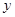 轴上,且过点
轴上,且过点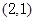 .
.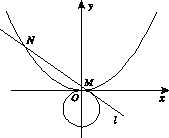
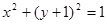 相切的直线
相切的直线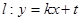 交抛物线于不同的两点
交抛物线于不同的两点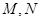 若抛物线上一点
若抛物线上一点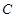 满足
满足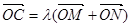
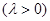 ,求
,求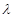 的取值范围.
的取值范围.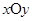 中,经过点
中,经过点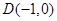 的动直线
的动直线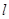 ,与椭圆
,与椭圆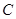 :
: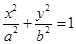 (
(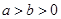 )相交于
)相交于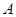 ,
,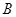 两点. 当
两点. 当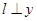 轴时,
轴时,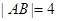 ,当
,当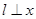 轴时,
轴时,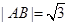 .
.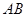 的中点为
的中点为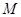 ,且
,且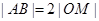 ,求直线
,求直线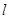 过椭圆
过椭圆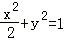 的左焦点F,且与椭圆相交于P、Q两点,M为PQ的中点,O为原点.若△FMO是以OF为底边的等腰三角形,则直线l的方程为 .
的左焦点F,且与椭圆相交于P、Q两点,M为PQ的中点,O为原点.若△FMO是以OF为底边的等腰三角形,则直线l的方程为 .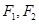 是双曲线
是双曲线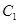 :
: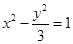 与椭圆
与椭圆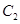 的公共焦点,点A是
的公共焦点,点A是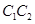 在第一象限的公共点.若
在第一象限的公共点.若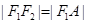 ,则
,则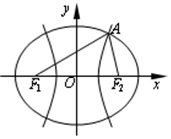
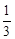
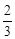
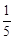
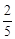
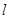 双曲线
双曲线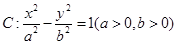 交
交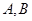 两点,若点
两点,若点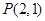 是
是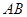 的中点,则
的中点,则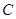 的离心率等于( )
的离心率等于( )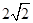
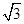
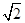
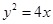 的焦点
的焦点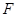 且倾斜角为
且倾斜角为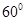 的直线
的直线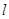 与抛物线在第一、四象限分别交于
与抛物线在第一、四象限分别交于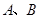 两点,则
两点,则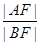 等于( )
等于( )