题目内容
已知f（x）是定义在（-∞，+∞）上的偶函数，且在（-∞，0]上是增函数，设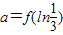
，
，则a，b，c，的大小关系是（ ）A．a＞b＞c
B．b＞a＞c
C．c＞a＞b
D．b＞c＞a
【答案】分析：根据偶函数在对称区间上单调性相反，可分析出f（x）在[0，+∞）上是减函数，根据偶函数的性质及指数函数和对数函数的性质，将三个自变量化到同一个单调区间上，并比较其大小，再根据函数的单调性可得答案．
解答：解：f（x）是定义在（-∞，+∞）上的偶函数，且在（-∞，0]上是增函数，
故f（x）在[0，+∞）上是减函数
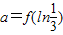=f（-ln3）=f（ln3），
c=f（0.4-1）=f（2.5）
∵2.5＞ln3＞log43
∴b＞a＞c
故选B
点评：本题考查的知识点是函数的奇偶性，函数的单调性，指数函数和对数函数的性质，是函数图象和性质的综合应用，难度中档．
解答：解：f（x）是定义在（-∞，+∞）上的偶函数，且在（-∞，0]上是增函数，
故f（x）在[0，+∞）上是减函数
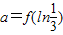=f（-ln3）=f（ln3），c=f（0.4-1）=f（2.5）
∵2.5＞ln3＞log43
∴b＞a＞c
故选B
点评：本题考查的知识点是函数的奇偶性，函数的单调性，指数函数和对数函数的性质，是函数图象和性质的综合应用，难度中档．
练习册系列答案
相关题目