题目内容
已知抛物线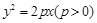 的焦点为
的焦点为 ,点
,点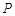 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
.
(Ⅰ)求抛物线的方程;
(Ⅱ) 设点 是抛物线上的两点,
是抛物线上的两点, 的角平分线与
的角平分线与 轴垂直,求
轴垂直,求 的面积最大时直线
的面积最大时直线 的方程.
的方程.
(Ⅰ)抛物线的方程为 ;(Ⅱ)所求直线
;(Ⅱ)所求直线 的方程为
的方程为 .
.
解析试题分析:(Ⅰ)由抛物线定义可求出 ;(Ⅱ)由
;(Ⅱ)由 的角平分线与
的角平分线与 轴垂直,可知
轴垂直,可知 的倾斜角互补,即
的倾斜角互补,即 的斜率互为相反数,可设
的斜率互为相反数,可设 的方程,利用设而不求的方法来求
的方程,利用设而不求的方法来求 的斜率为
的斜率为 ,设直线
,设直线 的方程
的方程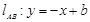 ,利用玄长公式与点到直线距离公式得
,利用玄长公式与点到直线距离公式得 的面积,由面积最大时来确定
的面积,由面积最大时来确定 ,从而得直线
,从而得直线 的方程.
的方程.
试题解析:(Ⅰ)解:设 ,因为
,因为 ,由抛物线的定义得
,由抛物线的定义得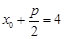 ,又
,又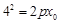 ,所以
,所以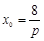 ,
,
因此 ,解得
,解得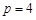 ,从而抛物线的方程为
,从而抛物线的方程为 ;
;
(Ⅱ)由(1)知点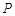 的坐标为
的坐标为 ,设
,设 ,因为
,因为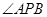 的角平分线与
的角平分线与 轴垂直,所以可知
轴垂直,所以可知 的倾斜角互补,即
的倾斜角互补,即 的斜率互为相反数,设直线
的斜率互为相反数,设直线 的斜率为
的斜率为 ,则
,则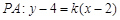 ,由题意
,由题意 ,把
,把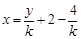 代入抛物线方程得
代入抛物线方程得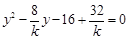 ,该方程的解为4、
,该方程的解为4、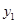 ,由韦达定理得
,由韦达定理得 ,即
,即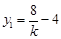 ,同理
,同理 ,所以
,所以 ,
,
设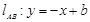 ,把
,把 代入抛物线方程得
代入抛物线方程得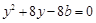 ,由题意
,由题意 ,且
,且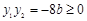 ,从而
,从而 ,又
,又 ,所以
,所以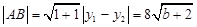 ,点
,点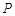 到
到 的距离
的距离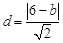 ,因此
,因此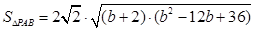 ,设
,设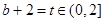 ,
,
则 ,
,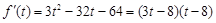 ,由
,由 知
知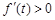 ,所以
,所以 在
在 上为增函数,因此
上为增函数,因此 ,即
,即 面积的最大值为
面积的最大值为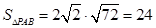 .
. 的面积取最大值时
的面积取最大值时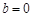 ,所求直线
,所求直线 的方程为
的方程为 .
.
考点:1、求抛物线方程,2、直线与二次曲线的位置关系,3、利用导数求最值.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
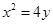 的对称轴上任一点
的对称轴上任一点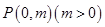 作直线与抛物线交于
作直线与抛物线交于 、
、 两点,点Q是点P关于原点的对称点.
两点,点Q是点P关于原点的对称点.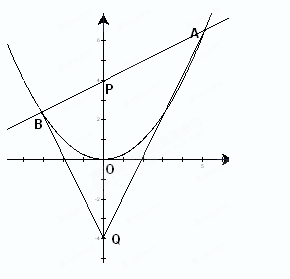
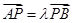 ,证明:
,证明: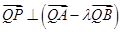 ;
;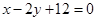 ,过
,过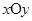 中,经过点
中,经过点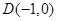 的动直线
的动直线 ,与椭圆
,与椭圆 :
: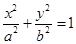 (
(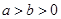 )相交于
)相交于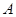 ,
,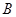 两点. 当
两点. 当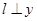 轴时,
轴时, ,当
,当 轴时,
轴时,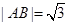 .
.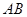 的中点为
的中点为 ,且
,且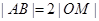 ,求直线
,求直线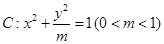 的左顶点为
的左顶点为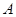 ,
,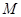 是椭圆
是椭圆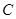 上异于点
上异于点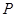 与点
与点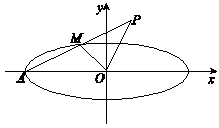
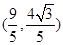 ,求
,求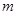 的值;
的值;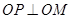 ,求
,求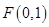 且与直线
且与直线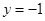 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为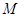 .点
.点 、
、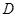 在轨迹
在轨迹 轴对称,过线段
轴对称,过线段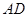 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线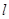 ,使直线
,使直线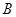 、
、 .
.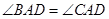 ;
;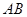 的距离等于
的距离等于 ,且△
,且△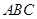 的面积为20,求直线
的面积为20,求直线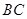 的方程.
的方程.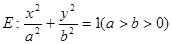 的离心率
的离心率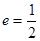 ,
,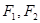 是其左右焦点,点
是其左右焦点,点 是直线
是直线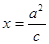 (其中
(其中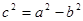 )上一点,且直线
)上一点,且直线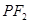 的倾斜角为
的倾斜角为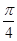 .
.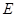 的方程;
的方程; 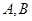 是椭圆
是椭圆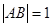 ,求
,求 (
( 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.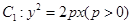 的焦点
的焦点 以及椭圆
以及椭圆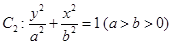 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆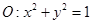 上.
上.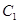 和椭圆
和椭圆 的标准方程;
的标准方程; 两不同点,交
两不同点,交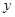 轴于点
轴于点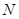 ,已知
,已知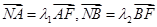 ,则
,则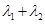
 与直线
与直线 相交于
相交于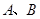 两点.
两点. ,直线
,直线 与
与 围成的矩形
围成的矩形 的面积为8,
的面积为8, (
(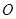 为坐标原点),求证:
为坐标原点),求证: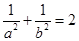 ;
;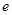 满足
满足 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.