题目内容
已知函数 ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.(1)当t=2时,求函数f(x)的单调递增区间;
(2)设|MN|=g(t),试求函数g(t)的表达式.
【答案】分析:(1)当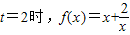 ,对函数求导,结合导数可求函数f(x)的单调递增区间
,对函数求导,结合导数可求函数f(x)的单调递增区间
(2)设M、N两点的横坐标分别为x1、x2,利用导数的几何意义可得切线MP的方程,由过(1,0)可,代入可得x1,x2满足x2+2tx-t=0.由方程的思想可得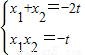 ,代入
,代入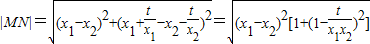
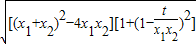 可求
可求
解答:解:(1)当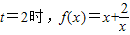 ,--------(2分)
,--------(2分)
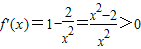
解得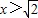 或
或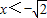 --------(4分)
--------(4分)
则函数f(x)有单调递增区间为 --------(5分)
--------(5分)
(2)设M、N两点的横坐标分别为x1、x2,
∵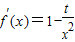
∴切线MP的方程为
∴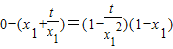 …(8分)
…(8分)
同理,由切线PN也过点(1,0),得x22+2tx2-t=0.
由(1)、(2),可得x1,x2是方程x2+2tx-t=0的两根,
∴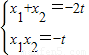 (*)
(*)
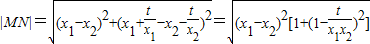
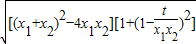
把(*)式代入,得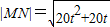 ,
,
因此,函数g(t)=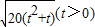 --------------(15分)
--------------(15分)
点评:本题主要考查了利用函数的导数求解函数的单调区间,及导数的几何意义:导数在某点处的导数值即为改点的切线的斜率的应用.
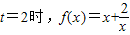 ,对函数求导,结合导数可求函数f(x)的单调递增区间
,对函数求导,结合导数可求函数f(x)的单调递增区间(2)设M、N两点的横坐标分别为x1、x2,利用导数的几何意义可得切线MP的方程,由过(1,0)可,代入可得x1,x2满足x2+2tx-t=0.由方程的思想可得
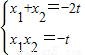 ,代入
,代入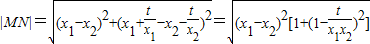
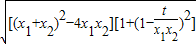 可求
可求解答:解:(1)当
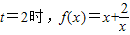 ,--------(2分)
,--------(2分)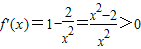
解得
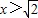 或
或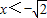 --------(4分)
--------(4分)则函数f(x)有单调递增区间为
 --------(5分)
--------(5分)(2)设M、N两点的横坐标分别为x1、x2,
∵
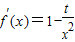
∴切线MP的方程为

∴
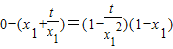 …(8分)
…(8分)同理,由切线PN也过点(1,0),得x22+2tx2-t=0.
由(1)、(2),可得x1,x2是方程x2+2tx-t=0的两根,
∴
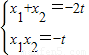 (*)
(*)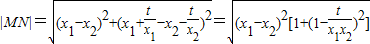
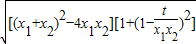
把(*)式代入,得
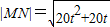 ,
,因此,函数g(t)=
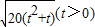 --------------(15分)
--------------(15分)点评:本题主要考查了利用函数的导数求解函数的单调区间,及导数的几何意义:导数在某点处的导数值即为改点的切线的斜率的应用.

练习册系列答案
相关题目
 ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值. ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值. ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值. ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.