题目内容
已知函数 ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.(1)当t=2时,求函数f(x)的单调递增区间;
(2)设|MN|=g(t),试求函数g(t)的表达式;
(3)在(2)的条件下,若对任意的正整数n,在区间
 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
【答案】分析:解此题的第一个突破点是第一(1)用导数的符号为正求单调区间,(2)求过切点的切线方程,找出两切点关系,再利用两点间的距离公式求解即可,(3)利用函数的单调性转化为恒成立问题.
解答:解:(1)当 ,
, 解得x>
解得x> ,或x<-
,或x<- .
.
∴函数f(x)有单调递增区间为 ,
,
(2)设M、N两点的横坐标分别为x1、x2,
∵ ,∴切线PM的方程为:
,∴切线PM的方程为: .
.
又∵切线PM过点P(1,0),∴有 .
.
即x12+2tx1-t=0.(1)
同理,由切线PN也过点(1,0),得x22+2tx2-t=0.(2)
由(1)、(2),可得x1,x2是方程x2+2tx-t=0的两根,
∴


把(*)式代入,得 ,
,
因此,函数g(t)的表达式为g(t)= (t>0)
(t>0)
(3)易知g(t)在区间 上为增函数,
上为增函数,
∴g(2)≤g(ai)(i=1,2,,m+1).
则m•g(2)≤g(a1)+g(a2)++g(am).
∵g(a1)+g(a2)++g(am)<g(am+1)对一切正整数n成立,
∴不等式m•g(2)<g(n+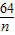 )对一切的正整数n恒成立
)对一切的正整数n恒成立 ,
,
即m< 对一切的正整数n恒成立
对一切的正整数n恒成立
∵ ,
,
∴ .
.
∴
由于m为正整数,∴m≤6.又当m=6时,存在a1=a2═am=2,am+1=16,对所有的n满足条件.
因此,m的最大值为6.
点评:本题第一问比较基础,二三问比较复杂,考切线问题,和数列问题,又渗透了恒成立思想,此题比较新,虽是压轴题但并不像以往压轴题的思路,有突破有创新,值得做.
解答:解:(1)当
 ,
, 解得x>
解得x> ,或x<-
,或x<- .
.∴函数f(x)有单调递增区间为
 ,
,
(2)设M、N两点的横坐标分别为x1、x2,
∵
 ,∴切线PM的方程为:
,∴切线PM的方程为: .
.又∵切线PM过点P(1,0),∴有
 .
.即x12+2tx1-t=0.(1)
同理,由切线PN也过点(1,0),得x22+2tx2-t=0.(2)
由(1)、(2),可得x1,x2是方程x2+2tx-t=0的两根,
∴



把(*)式代入,得
 ,
,因此,函数g(t)的表达式为g(t)=
 (t>0)
(t>0)(3)易知g(t)在区间
 上为增函数,
上为增函数,∴g(2)≤g(ai)(i=1,2,,m+1).
则m•g(2)≤g(a1)+g(a2)++g(am).
∵g(a1)+g(a2)++g(am)<g(am+1)对一切正整数n成立,
∴不等式m•g(2)<g(n+
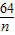 )对一切的正整数n恒成立
)对一切的正整数n恒成立 ,
,即m<
 对一切的正整数n恒成立
对一切的正整数n恒成立∵
 ,
,∴
 .
.∴

由于m为正整数,∴m≤6.又当m=6时,存在a1=a2═am=2,am+1=16,对所有的n满足条件.
因此,m的最大值为6.
点评:本题第一问比较基础,二三问比较复杂,考切线问题,和数列问题,又渗透了恒成立思想,此题比较新,虽是压轴题但并不像以往压轴题的思路,有突破有创新,值得做.

练习册系列答案
相关题目
 ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值. ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值. ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N. 内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内,总存在m+1个数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.