Question

家具公司制作木质的书桌和椅子，需要木工和漆工两道工序，已知木工平均四个小时做一把椅子，八个小时做一张书桌，该公司每星期木工最多有8000个工作时；漆工平均两小时漆一把椅子、一小时漆一张书桌，该公司每星期漆工最多有1300个工作时，又已知制作一把椅子和一张书桌的利润分别是15元和20元，试根据以上条件，问怎样安排生产能获得最大利润？

Answer 1

答案：
解析：

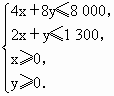解：生产200把椅子、900张书桌可获得最大利润21000元(点拨：设每星期生产x把椅子、y张书桌，那么利润P＝15x＋20y，而x、y必须满足约束条件在直角坐标系内作出它表示的区域，它围成一个封闭的四边形，其四个顶点分别为(0，0)，(650，0)，(200，900)，(0，1000)，而直线P＝15x＋20y，当P变化时，它是一组斜率为－的平行直线，当纵截距最大时，利润亦最大，在上述区域内平行移动的直线，易见当直线过点(200，900)时，P值最大．