题目内容
某家具公司制作木质的书桌和椅子两种家具，需要木工和漆工两道工序，已知木工平均四个小时做一把椅子，八个小时做一张书桌，该公司每星期木工最多有8 000个工作时；漆工平均两小时漆一把椅子，一个小时漆一张书桌，该公司每星期漆工最多有1 300个工作时.又已知制作一把椅子和一张书桌的利润分别是15元和20元，根据以上条件，怎样安排生产能获得最大利润？
生产200把椅子、900张书桌可获得最大利润21 000元.
解析:
依题意设每星期生产x把椅子，y张书桌，
那么利润p=15x+20y.
其中x,y满足限制条件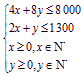
.
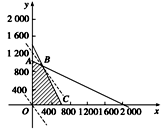
即点（x,y）的允许区域为图中阴影部分，它们的边界分别为4x+8y=8 000 (即AB)，2x+y=1 300(即BC)，x=0(即OA)和y=0(即OC）.
对于某一个确定的
=
满足=15x+20y,且点（x,y)属于
解x,y就是一个能获得元利润的生产方案.
对于不同的p,p=15x+20y表示一组斜率为-
的平行线，且p越大，相应的直线位置越高；p越小，相应的直线位置越低.按题意，要求p的最大值，需把直线p=15x＋20y尽量地往上平移，又考虑到x，y的允许范围，
当直线通过B点时，处在这组平行线的最高位置，此时p取最大值.
由
,得B（200，900），
当x=200,y=900时，p取最大值，
即pmax=15×200+20×900=21 000,
即生产200把椅子、900张书桌可获得最大利润21 000元.
练习册系列答案
相关题目