题目内容
(本小题满分10分)选修4-4:坐标系统与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为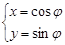 (
(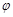 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为 (
(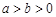 ,
,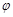 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=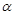 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当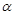 =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当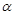 =
=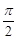 时,这两个交点重合.
时,这两个交点重合.
(I)分别说明C1,C2是什么曲线,并求出a与b的值;
(II)设当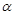 =
= 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当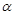 =
= 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
【答案】
解:(I)C1是圆,C2是椭圆.
当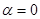 时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,所以a=3.
时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,所以a=3.
当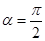 时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
(II)C1,C2的普通方程分别为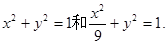
当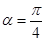 时,射线l与C1交点A1的横坐标为
时,射线l与C1交点A1的横坐标为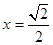 ,与C2交点B1的横坐标为
,与C2交点B1的横坐标为

当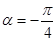 时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此,
时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此,
四边形A1A2B2B1为梯形.
故四边形A1A2B2B1的面积为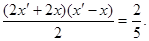 …………10分
…………10分
【解析】略

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,