题目内容
必做题:(本小题满分10分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
已知an(n∈N*)是二项式(2+x)n的展开式中x的一次项的系数.
(Ⅰ)求an;
(Ⅱ)是否存在等差数列{bn},使an=b1cn1+b2cn2+b3cn3+…+bncnn对一切正整数n都成立?并证明你的结论.
已知an(n∈N*)是二项式(2+x)n的展开式中x的一次项的系数.
(Ⅰ)求an;
(Ⅱ)是否存在等差数列{bn},使an=b1cn1+b2cn2+b3cn3+…+bncnn对一切正整数n都成立?并证明你的结论.
分析:(I)结合((2+x)n的展开式的通项Tr+1=Cnr2n-rxr,令r=1可得an=Cnr2n-r=n•2n-1
(II)若存在等差数列{bn},满足已知条件则把n=1,n=2,n=3分别代入可求b1,b2,b3,结合所求可猜想bn=n
再证明:an=b1Cn1+b2Cn2+…+bnCnn对一切正整数n都成立
(法一)设S=Cn1+2Cn2+…+nCnn,则S=nCnn+(n-1)Cnn-1+…+Cn1,利用倒序相加结合组合数的性质可证
(法二)利用组合数的性质kCnk=nCn-1k-1,对原式化简可证
(II)若存在等差数列{bn},满足已知条件则把n=1,n=2,n=3分别代入可求b1,b2,b3,结合所求可猜想bn=n
再证明:an=b1Cn1+b2Cn2+…+bnCnn对一切正整数n都成立
(法一)设S=Cn1+2Cn2+…+nCnn,则S=nCnn+(n-1)Cnn-1+…+Cn1,利用倒序相加结合组合数的性质可证
(法二)利用组合数的性质kCnk=nCn-1k-1,对原式化简可证
解答:解:(I)∵((2+x)n的展开式的通项为:Tr+1=Cnr2n-rxr(r=0,1,2…n)
令r=1可得an=Cnr2n-r=n•2n-1
(II)若存在等差数列{bn},满足已知条件
则当n=1时,b1=a1=1
当n=2时,a2=b1C21+b2C22即4=4=2+b2,所以b2=2
当n=3时,a3=b1C31+b2C32+b3C33即12=3+6+b3,所以b3=3
由上述结果,猜想bn=n
下面证明:当bn=n时,an=b1Cn1+b2Cn2+…+bnCnn对一切正整数n都成立
即证n•2n-1=Cn1+2Cn2+…+nCnn成立
(法一)设S=Cn1+2Cn2+…+nCnn
S=nCnn+(n-1)Cnn-1+…+Cn1
则2S=nCn0+nCn1+…+nCnn=n(Cn0+Cn1+…+Cnn)=n•2n
∴S=n•2n-1
即n•2n-1=Cn1+2Cn2+…+nCnn成立
(法二)∵kCnk=k
=
=n
=nCn-1k-1
∴Cn1+2Cn2+…+nCnn=n(Cn-10+Cn-11+…+Cn-1n-1)=n•2n-1
综上可得,存在等差数列bn=n满足已知条件.
令r=1可得an=Cnr2n-r=n•2n-1
(II)若存在等差数列{bn},满足已知条件
则当n=1时,b1=a1=1
当n=2时,a2=b1C21+b2C22即4=4=2+b2,所以b2=2
当n=3时,a3=b1C31+b2C32+b3C33即12=3+6+b3,所以b3=3
由上述结果,猜想bn=n
下面证明:当bn=n时,an=b1Cn1+b2Cn2+…+bnCnn对一切正整数n都成立
即证n•2n-1=Cn1+2Cn2+…+nCnn成立
(法一)设S=Cn1+2Cn2+…+nCnn
S=nCnn+(n-1)Cnn-1+…+Cn1
则2S=nCn0+nCn1+…+nCnn=n(Cn0+Cn1+…+Cnn)=n•2n
∴S=n•2n-1
即n•2n-1=Cn1+2Cn2+…+nCnn成立
(法二)∵kCnk=k
| n! |
| k!(n-k)! |
| n! |
| (k-1)!(n-k)! |
| (n-1)! |
| (k-1)![(n-1)-(k-1)]! |
∴Cn1+2Cn2+…+nCnn=n(Cn-10+Cn-11+…+Cn-1n-1)=n•2n-1
综上可得,存在等差数列bn=n满足已知条件.
点评:本题主要考查了利用二项展开式的通项求解指定项的系数,考查了组合数的两个性质:①Cn0+Cn1+…+Cnn=2n②kCnk=nCn-1k-1的综合应用及倒序求和、数学归纳法证明数学命题等知识的综合应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
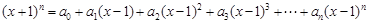 ,(其中
,(其中 )
)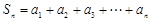 .
.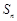 ;
;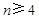 时,
时,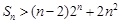 .
.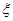 的分布列,并计算其数学期望.
的分布列,并计算其数学期望.