题目内容
(2012•太原模拟)设函数f(x)=a(x+
)+2lnx,g(x)=x2.
(1)若a=
时,直线l与函数f(x)和函数g(x)的图象相切于同一点,求切线l的方程;
(2)若f(x)在[2,4]内为单调函数,求实数a的取值范围.
说明:请考生在第22、23、24三题中任选一题作答,如果多做,则按所做第一题记分.
| 1 |
| x |
(1)若a=
| 1 |
| 2 |
(2)若f(x)在[2,4]内为单调函数,求实数a的取值范围.
说明:请考生在第22、23、24三题中任选一题作答,如果多做,则按所做第一题记分.
分析:(1)由f(x)求出其导函数,把切点的横坐标代入导函数中即可表示出切线的斜率,两次求出的斜率相等列出关于切点的横坐标x的方程,求出切点的坐标,根据得出的切点坐标,同时由f(x)求出其导函数,把切点的横坐标代入导函数中即可表示出切线的斜率,根据切点坐标和切线过原点写出切线方程即可.
(2)通过解f′(x),求其单调区间,转化为恒成立问题求a的取值范围.
(2)通过解f′(x),求其单调区间,转化为恒成立问题求a的取值范围.
解答:解:(1)若a=
时,
∵f′(x)=
(1-
)+
=
,g'(x)=2x
因为直线l与函数f(x)、g(x)的图象相切于同一点,
从而有:
=2x(4分)
解得x=1,x=
,(x=-1不在定义域内,故舍去)
又f'(1)=2,f(1)=1,
f′(
)=
,f(
)=
,
g'(1)=2,g(1)=1;
g′(
)=
,g(
)=
.
①当x=1时,则l的方程为:y=2x-1
②当x=
时,又因为点(
,
)也在f(x)的图象上,
所以l的方程为y=
x-
.
综上所述直线l的方程为y=2x-1或y=
x-
.
(2)∵f′(x)=a(1-
)+
=
,
要使f(x)在[2,4]为单调增函数,则f′(x)≥0在[2,4]恒成立,
即
≥0在[2,4]恒成立,即ax2+2x-a≥0在[2,4]恒成立,
又a(x2-1)≥-2x即a≥
=
(2≤x≤4)(8分)
设u(x)=
-x(2≤x≤4),
因为u′(x)=-
-1<0(x>0),
所以u(x)在(0,+∞)上单调递减.
∴当2≤x≤4时,
∈[-
,-
]
所以要使a≥
=
(2≤x≤4),
只须当a≥-
时即可,(10分)
同理要为f(x)单调减函数,则f′(x)≤0在[2,4]恒成立,
易得a≤-
,
综上,f(x)在[2,4]为单调函数,
则a的取值范围为a≤-
或a≥-
(12分).
| 1 |
| 2 |
∵f′(x)=
| 1 |
| 2 |
| 1 |
| x2 |
| 2 |
| x |
| x2+4x-1 |
| 2x2 |
因为直线l与函数f(x)、g(x)的图象相切于同一点,
从而有:
| x2+4x-1 |
| 2x2 |
解得x=1,x=
| 1 |
| 4 |
又f'(1)=2,f(1)=1,
f′(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
g'(1)=2,g(1)=1;
g′(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
①当x=1时,则l的方程为:y=2x-1
②当x=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
所以l的方程为y=
| 1 |
| 2 |
| 1 |
| 16 |
综上所述直线l的方程为y=2x-1或y=
| 1 |
| 2 |
| 1 |
| 16 |
(2)∵f′(x)=a(1-
| 1 |
| x2 |
| 2 |
| x |
| ax2+2x-a |
| x2 |
要使f(x)在[2,4]为单调增函数,则f′(x)≥0在[2,4]恒成立,
即
| ax2+2x-a |
| x2 |
又a(x2-1)≥-2x即a≥
| 2x |
| 1-x2 |
| 2 | ||
|
设u(x)=
| 1 |
| x |
因为u′(x)=-
| 1 |
| x2 |
所以u(x)在(0,+∞)上单调递减.
∴当2≤x≤4时,
| 2 | ||
|
| 4 |
| 3 |
| 8 |
| 15 |
所以要使a≥
| 2x |
| 1-x2 |
| 2 | ||
|
只须当a≥-
| 8 |
| 15 |
同理要为f(x)单调减函数,则f′(x)≤0在[2,4]恒成立,
易得a≤-
| 4 |
| 3 |
综上,f(x)在[2,4]为单调函数,
则a的取值范围为a≤-
| 4 |
| 3 |
| 8 |
| 15 |
点评:对于已知函数单调性,求参数范围问题的常见解法;设函数f(x)在(a,b)上可导,若f(x)在(a,b)上是增函数,则可得f′(x)≥0,从而建立了关于待求参数的不等式,同理,若f(x)在(a,b)上是减函数,,则可得f′(x)≤0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
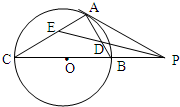 (2012•太原模拟)选修4-1:几何证明选讲
(2012•太原模拟)选修4-1:几何证明选讲