题目内容
已知函数f(x)=|x2-k-1|-kx.
(1)若k=1,求方程f(x)=0的解;
(2)若k>0,不等式f(x)≤0的解集为A,
①求集合A;
②若集合B={x|(x-1)(x-2)(x-3k)≥0},A⊆B,求实数k的取值范围.
(1)若k=1,求方程f(x)=0的解;
(2)若k>0,不等式f(x)≤0的解集为A,
①求集合A;
②若集合B={x|(x-1)(x-2)(x-3k)≥0},A⊆B,求实数k的取值范围.
分析:(1)若k=1,函数f(x)=|x2-2|-x,分 x2 ≥2和 x2 <2两种情况分别求出方程f(x)=0的解.
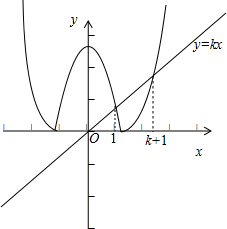
(2)①若k>0,不等式即|x2-k-1|≤kx,结合图象 不等式f(x)≤0的解集 A={x|1≤x≤k+1}.
②分0<3k<1、3k=1、2>3k>1、3k=2、3k>2五种情况分别求出集合B,由A⊆B求出k的范围,最后取并集,即得所求.
(2)①若k>0,不等式即|x2-k-1|≤kx,结合图象 不等式f(x)≤0的解集 A={x|1≤x≤k+1}.
②分0<3k<1、3k=1、2>3k>1、3k=2、3k>2五种情况分别求出集合B,由A⊆B求出k的范围,最后取并集,即得所求.
解答:解:(1)若k=1,函数f(x)=|x2-k-1|-kx=|x2-2|-x.
当 x2 ≥2时,f(x)=x2-2-x,由f(x)=0 解得 x=-1 或 x=2(舍去).
当 x2 <2时,f(x)=2-x2 -x,f(x)=0 解得 x=-2(舍去)或x=1.
综上,x=-1 或x=1.
(2)若k>0,不等式f(x)≤0,即|x2-k-1|≤kx.
①由|x2-k-1|=kx,解得 x=1 或 x=k+1,结合图象可得 方程|x2-k-1|=kx 的解为x=1 和 x=k+1,
故不等式f(x)≤0的解集 A={x|1≤x≤k+1}.
②若集合B={x|(x-1)(x-2)(x-3k)≥0},A={x|1≤x≤k+1}
当 0<3k<1时,B={x|1≥x≥3k 或 x≥2},由A⊆B 可得 k不存在.
当3k=1时,B={x|x≥2},A⊆B不可能.
当2>3k>1时,B={x|3k≥x≥1 或 x≥2},由A⊆B 可得k+1≤3k,k≥
,从而可得
>k≥
.
当3k=2时,B={x|x≥1},A⊆B 恒成立,故 k=
满足条件.
当3k>2时,B={x|x≥3k 或1≤x≤2},由A⊆B 可得k+1≤2,k≤1,从而可得1≥k>
.
综上可得 1≥k≥
,故实数k的取值范围为[
,1].
当 x2 ≥2时,f(x)=x2-2-x,由f(x)=0 解得 x=-1 或 x=2(舍去).
当 x2 <2时,f(x)=2-x2 -x,f(x)=0 解得 x=-2(舍去)或x=1.
综上,x=-1 或x=1.
(2)若k>0,不等式f(x)≤0,即|x2-k-1|≤kx.
①由|x2-k-1|=kx,解得 x=1 或 x=k+1,结合图象可得 方程|x2-k-1|=kx 的解为x=1 和 x=k+1,
故不等式f(x)≤0的解集 A={x|1≤x≤k+1}.

②若集合B={x|(x-1)(x-2)(x-3k)≥0},A={x|1≤x≤k+1}
当 0<3k<1时,B={x|1≥x≥3k 或 x≥2},由A⊆B 可得 k不存在.
当3k=1时,B={x|x≥2},A⊆B不可能.
当2>3k>1时,B={x|3k≥x≥1 或 x≥2},由A⊆B 可得k+1≤3k,k≥
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
当3k=2时,B={x|x≥1},A⊆B 恒成立,故 k=
| 2 |
| 3 |
当3k>2时,B={x|x≥3k 或1≤x≤2},由A⊆B 可得k+1≤2,k≤1,从而可得1≥k>
| 2 |
| 3 |
综上可得 1≥k≥
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查集合关系中参数的取值范围问题,带有绝对值得函数的研究方法,体现了分类讨论及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|