题目内容
6．若（2x+3）3=a0+a1（x+2）+a2（x+2）2+a3（x+2）3，则a0+a1+2a2+3a3=17．分析 由条件，再结合（2x+3）3 =8•${[-\frac{1}{2}+（x+2）]}^{3}$=8[-$\frac{1}{8}$+$\frac{1}{4}$•（x+2）-$\frac{1}{2}$•（x+2）2+（x+2）3]，求得a0、a1、2a2、a3的值，可得a0+a1+2a2+3a3的值．
解答 解：∵（2x+3）3=a0+a1（x+2）+a2（x+2）2+a3（x+2）3，
（2x+3）3=${[2（x+\frac{3}{2}）]}^{3}$=8•${[-\frac{1}{2}+（x+2）]}^{3}$=8[-$\frac{1}{8}$+$\frac{1}{4}$•（x+2）-$\frac{1}{2}$•（x+2）2+（x+2）3]，
∴a0=-1，a1=2，a2 =-4，a3=8，∴a0+a1+2a2+3a3=17，
故答案为：17．
点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
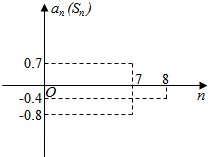已知等差数列{an}的前n项和为Sn，在同一坐标系中，an=f（n）及Sn=g（n）的部分图象如图所示．