题目内容
(本题满分14分)
已知函数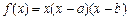 ,点
,点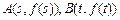 .
.
(Ⅰ)若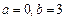 ,函数
,函数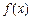 在
在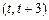 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求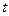 的取值范围;
的取值范围;
(Ⅱ) 当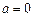 时,
时,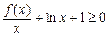 对任意的
对任意的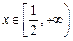 恒成立,求
恒成立,求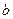 的取值范围;
的取值范围;
(Ⅲ)若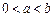 ,函数
,函数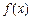 在
在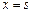 和
和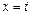 处取得极值,且
处取得极值,且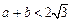 ,
,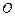 是坐标原点,证明:直线
是坐标原点,证明:直线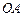 与直线
与直线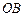 不可能垂直.
不可能垂直.
已知函数
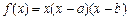 ,点
,点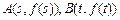 .
.(Ⅰ)若
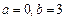 ,函数
,函数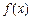 在
在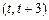 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求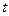 的取值范围;
的取值范围;(Ⅱ) 当
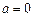 时,
时,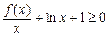 对任意的
对任意的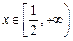 恒成立,求
恒成立,求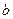 的取值范围;
的取值范围;(Ⅲ)若
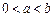 ,函数
,函数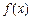 在
在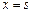 和
和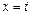 处取得极值,且
处取得极值,且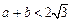 ,
,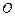 是坐标原点,证明:直线
是坐标原点,证明:直线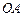 与直线
与直线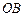 不可能垂直.
不可能垂直.解:(Ⅰ)当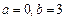 时,
时, ,
,
令 得
得 ,根据导数的符号可以得出函数
,根据导数的符号可以得出函数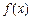 在
在 处取得极大值,
处取得极大值,
在 处取得极小值.函数
处取得极小值.函数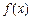 在
在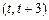 上既能取到极大值,又能取到极小值,
上既能取到极大值,又能取到极小值,
则只要 且
且 即可,即只要
即可,即只要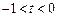 即可.
即可.
所以 的取值范围是
的取值范围是 . ………… 4分
. ………… 4分
(Ⅱ)当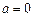 时,
时,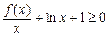 对任意的
对任意的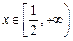 恒成立,
恒成立,
即 对任意的
对任意的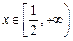 恒成立,
恒成立,
也即 在对任意的
在对任意的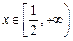 恒成立.
恒成立.
令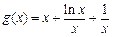 ,则
,则 . ………… 6分
. ………… 6分
记 ,则
,则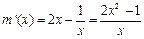 ,
,
则这个函数在其定义域内有唯一的极小值点 ,
,
故也是最小值点,所以 ,
,
从而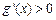 ,所以函数
,所以函数 在
在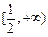 单调递增.
单调递增.
函数 .故只要
.故只要 即可.
即可.
所以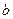 的取值范围是
的取值范围是 ………… 9分
………… 9分
(Ⅲ)假设 ,即
,即 ,
,
即 ,
,
故 ,
,
即 .
.
由于 是方程
是方程 的两个根,
的两个根,
故 .代入上式得
.代入上式得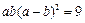 . ………… 12分
. ………… 12分
 ,
,
即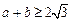 ,与
,与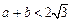 矛盾,
矛盾,
所以直线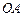 与直线
与直线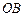 不可能垂直. ………… 14分
不可能垂直. ………… 14分
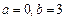 时,
时, ,
,令
 得
得 ,根据导数的符号可以得出函数
,根据导数的符号可以得出函数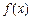 在
在 处取得极大值,
处取得极大值,在
 处取得极小值.函数
处取得极小值.函数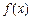 在
在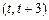 上既能取到极大值,又能取到极小值,
上既能取到极大值,又能取到极小值,则只要
 且
且 即可,即只要
即可,即只要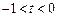 即可.
即可.所以
 的取值范围是
的取值范围是 . ………… 4分
. ………… 4分 (Ⅱ)当
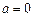 时,
时,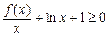 对任意的
对任意的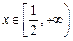 恒成立,
恒成立,即
 对任意的
对任意的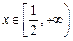 恒成立,
恒成立,也即
 在对任意的
在对任意的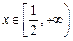 恒成立.
恒成立. 令
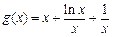 ,则
,则 . ………… 6分
. ………… 6分记
 ,则
,则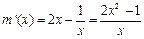 ,
,则这个函数在其定义域内有唯一的极小值点
 ,
,故也是最小值点,所以
 ,
,从而
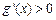 ,所以函数
,所以函数 在
在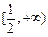 单调递增.
单调递增.函数
 .故只要
.故只要 即可.
即可.所以
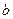 的取值范围是
的取值范围是 ………… 9分
………… 9分 (Ⅲ)假设
 ,即
,即 ,
,即
 ,
,故
 ,
,即
 .
.由于
 是方程
是方程 的两个根,
的两个根,故
 .代入上式得
.代入上式得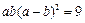 . ………… 12分
. ………… 12分  ,
,即
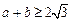 ,与
,与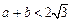 矛盾,
矛盾,所以直线
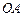 与直线
与直线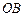 不可能垂直. ………… 14分
不可能垂直. ………… 14分略

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 ,若不等式
,若不等式 的解集为
的解集为 。
。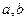 的值;
的值; 在
在
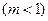 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。 的解集
的解集 是
是  .
. 则
则 的大小关系为 (用 “<”连接)
的大小关系为 (用 “<”连接)  ,则
,则 =" " .
=" " . 果用此材料 在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图所示),则围成的矩形最大面积为________.(围墙厚度不计)
果用此材料 在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图所示),则围成的矩形最大面积为________.(围墙厚度不计) 
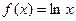 .
.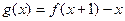 的最大值;
的最大值;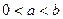 时,求证
时,求证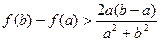 .
. 的定义域用区间表示应为 ▲
的定义域用区间表示应为 ▲