题目内容
设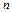 为正整数,规定:
为正整数,规定: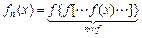 ,已知
,已知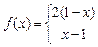

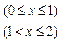 .
.
(1)解不等式: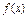 ≤
≤ ;
;
(2)设集合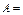 {0,1,2},对任意
{0,1,2},对任意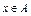 ,证明:
,证明: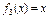 ;
;
(3)探求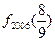 ;
;
(4)若集合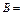 {
{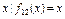 ,
,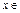 [0,2]},证明:
[0,2]},证明: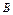 中至少包含有8个元素.
中至少包含有8个元素.
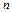 为正整数,规定:
为正整数,规定: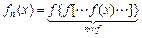 ,已知
,已知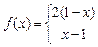

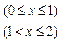 .
.(1)解不等式:
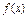 ≤
≤ ;
;(2)设集合
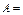 {0,1,2},对任意
{0,1,2},对任意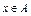 ,证明:
,证明: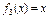 ;
;(3)探求
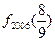 ;
;(4)若集合
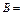 {
{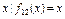 ,
,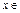 [0,2]},证明:
[0,2]},证明: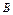 中至少包含有8个元素.
中至少包含有8个元素.(1){ |
| ≤
≤ ≤2}(2)见解析(3)
≤2}(2)见解析(3)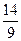 (4)见解析
(4)见解析
 |
| ≤
≤ ≤2}(2)见解析(3)
≤2}(2)见解析(3)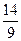 (4)见解析
(4)见解析(1)①当0≤ ≤1时,由
≤1时,由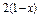 ≤
≤ 得,
得, ≥
≥ .∴
.∴ ≤
≤ ≤1.
≤1.
②当1< ≤2时,因
≤2时,因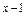 ≤
≤ 恒成立.∴1<
恒成立.∴1< ≤2.
≤2.
由①,②得,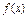 ≤
≤ 的解集为{
的解集为{ |
| ≤
≤ ≤2}.
≤2}.
(2)∵ ,
,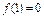 ,
, ,
,
∴当 时,
时,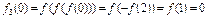 ;
;
当 时,
时,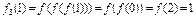 ;
;
当 时,
时,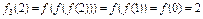 .
.
即对任意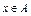 ,恒有
,恒有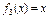 .
.
(3)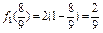 ,
,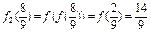 ,
,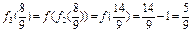 ,
,
 ,……
,……
一般地,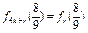 (
( N).
N).
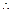
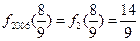 .
.
(4)由(1)知, ,∴
,∴ .则
.则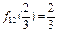 .∴
.∴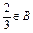 .
.
由(2)知,对 ,或1,或2,恒有
,或1,或2,恒有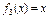 ,∴
,∴ .则0,1,2
.则0,1,2 .
.
由(3)知,对 ,
,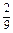 ,
,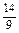 ,
, ,恒有
,恒有 ,∴
,∴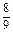 ,
,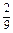 ,
,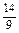 ,
,
 .
.
综上所述, ,0,1,2,
,0,1,2,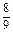 ,
,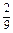 ,
,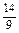 ,
,
 .∴
.∴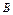 中至少含有8个元素.
中至少含有8个元素.
 ≤1时,由
≤1时,由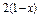 ≤
≤ 得,
得, ≥
≥ .∴
.∴ ≤
≤ ≤1.
≤1.②当1<
 ≤2时,因
≤2时,因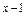 ≤
≤ 恒成立.∴1<
恒成立.∴1< ≤2.
≤2.由①,②得,
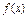 ≤
≤ 的解集为{
的解集为{ |
| ≤
≤ ≤2}.
≤2}.(2)∵
 ,
,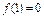 ,
, ,
,∴当
 时,
时,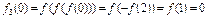 ;
;当
 时,
时,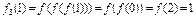 ;
;当
 时,
时,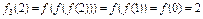 .
.即对任意
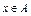 ,恒有
,恒有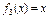 .
.(3)
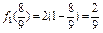 ,
,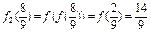 ,
,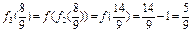 ,
, ,……
,……一般地,
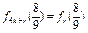 (
( N).
N).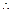
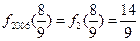 .
.(4)由(1)知,
 ,∴
,∴ .则
.则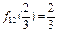 .∴
.∴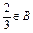 .
.由(2)知,对
 ,或1,或2,恒有
,或1,或2,恒有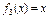 ,∴
,∴ .则0,1,2
.则0,1,2 .
.由(3)知,对
 ,
,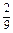 ,
,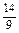 ,
, ,恒有
,恒有 ,∴
,∴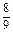 ,
,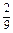 ,
,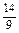 ,
,
 .
.综上所述,
 ,0,1,2,
,0,1,2,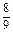 ,
,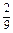 ,
,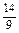 ,
,
 .∴
.∴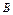 中至少含有8个元素.
中至少含有8个元素.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
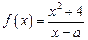
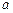 为非零常数,解不等式
为非零常数,解不等式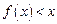 ;
;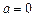 时,不等式
时,不等式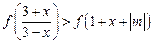 在
在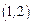 上有解,求
上有解,求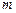 的取值范围.
的取值范围.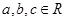 ,
,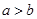 ,则下列不等式成立的是( )
,则下列不等式成立的是( )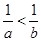
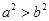
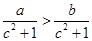
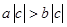
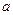 克,商家称其中黄金含量不低于
克,商家称其中黄金含量不低于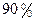 ,黄金和白银的密度分别是
,黄金和白银的密度分别是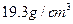 和
和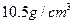 ,列出不等式表示这件首饰的体积
,列出不等式表示这件首饰的体积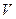 应满足的不等关系是 .
应满足的不等关系是 .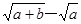 ,y=
,y=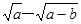 ,则x、y的大小关系为( )
,则x、y的大小关系为( ) 的解集不是空集,则实数a的取值范围是__________.
的解集不是空集,则实数a的取值范围是__________.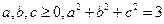 ,则
,则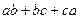 的最大值为( ).
的最大值为( ).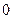
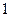
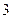
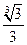
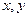 满足
满足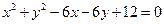 ,则
,则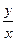 的最大值为
的最大值为 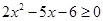 成立的一个充分不必要条件是
成立的一个充分不必要条件是