题目内容
已知向量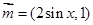 ,
, ,函数
,函数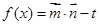 .
.
(Ⅰ)若方程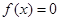 在
在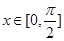 上有解,求
上有解,求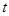 的取值范围;
的取值范围;
(Ⅱ)在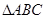 中,
中,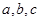 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的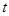 取最大值且
取最大值且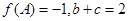 时,求
时,求 的最小值.
的最小值.
(Ⅰ)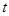 的取值范围
的取值范围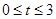 ;(Ⅱ)
;(Ⅱ) 的最小值
的最小值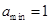 .
.
解析试题分析:(Ⅰ)由向量数量积转化为三角函数,利用倍角公式将角转化为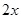 的三角函数,然后利用
的三角函数,然后利用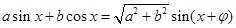 可以得到
可以得到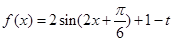 ,方程
,方程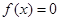 在
在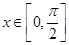 有解,即
有解,即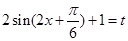 有根问题,从而转化为求
有根问题,从而转化为求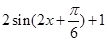 值域;(Ⅱ)由
值域;(Ⅱ)由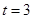 ,且
,且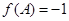 ,代入
,代入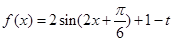 ,可求出
,可求出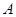 的值,再由
的值,再由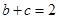 ,可想到利用余弦定律来解.
,可想到利用余弦定律来解.
试题解析:
(1)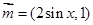 ,
, ,函数
,函数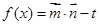
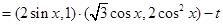
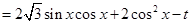
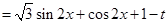
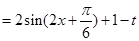 ,
,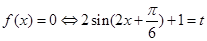 , 当
, 当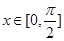 时,
时,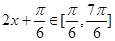 ,
,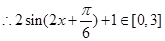 ,
, 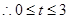 .
.
(Ⅱ)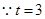 ,且
,且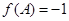 ,代入
,代入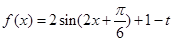 ,得
,得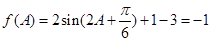 ,
,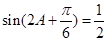 ,
,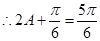 或
或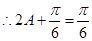 ,而
,而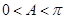 ,解得
,解得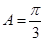 ,由余弦定律可得
,由余弦定律可得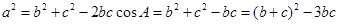 ,
,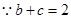 ,
,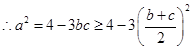
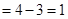 .
.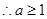 ,故
,故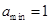 .
.
考点:1、向量数量积,2、三角恒等变换,3、方程的根的问题,4、余弦定理,5、基本不等式.

练习册系列答案
相关题目
设 ,当
,当 时,
时,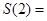 ( )
( )
A.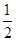 | B.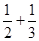 | C.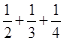 | D.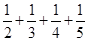 |
在数列 中,
中,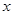 等于( )
等于( )
A. | B.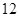 | C.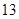 | D.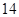 |
数列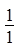 、
、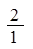 、
、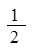 、
、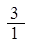 、
、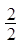 、
、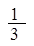 、
、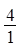 、
、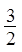 、
、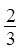 、
、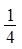 ……依次排列到第
……依次排列到第 项属于的范围是( )。
项属于的范围是( )。
A.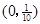 | B.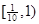 | C.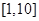 | D.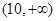 |
 ,θ为a与b的夹角.
,θ为a与b的夹角. sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间. 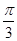 ,求△ABC的面积.
,求△ABC的面积.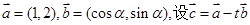 (
( 为实数).
为实数).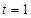 时,若
时,若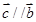 ,求
,求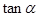 ;
;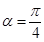 ,求
,求 的最小值,并求出此时向量
的最小值,并求出此时向量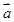 在
在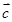 方向上的投影.
方向上的投影.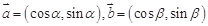 ,其中
,其中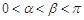 .
. 与
与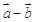 互相垂直;
互相垂直;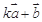 与
与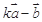 大小相等,求
大小相等,求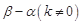 .
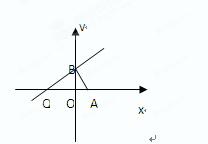
.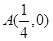 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若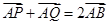 ,
,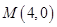 .
.
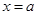 ,以PM为直径的圆与直线
,以PM为直径的圆与直线