题目内容
设函数f(x)=x|x-a|,若对于任意的x1,x2∈[2,+∞),x1≠x2,不等式 >0恒成立,则实数a的取值范围是________.
>0恒成立,则实数a的取值范围是________.
(-∞,2]
分析:首先由函数单调性定义,判断f(x)=x|x-a|在[2,+∞)上单调递增;然后把a分成a≤2与a>2两种情况分别进行检验,从而得出结论.
解答:∵函数f(x)=x|x-a|=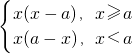 ,对于任意的x1,x2∈[2,+∞),x1≠x2,不等式
,对于任意的x1,x2∈[2,+∞),x1≠x2,不等式 >0恒成立,
>0恒成立,
故函数在[2,+∞)上是增函数.
(1)当a≤2时,
若x∈[2,+∞),则f(x)=x(x-a)=x2-ax,其对称轴为x= ,此时
,此时 <2,所以,f(x)在[2,+∞)上是递增的.
<2,所以,f(x)在[2,+∞)上是递增的.
(2)当a>2时,
①若x∈[a,+∞),则f(x)=x(x-a)=x2-ax,由于其对称轴为x= ,所以f(x)在[a,+∞)上是递增的;
,所以f(x)在[a,+∞)上是递增的;
②若x∈[2,a),则f(x)=x(a-x)=-x2+ax,其对称轴为x= ,所以f(x)在[
,所以f(x)在[ ,a)上是递减的,
,a)上是递减的,
因此f(x)在[2,a)上必有递减区间,故不满足条件.
综合(1)、(2)可知a≤2,
故答案为 (-∞,2].
点评:本题考查了函数单调性的定义,同时考查了分类讨论的思想方法,属于基础题.
分析:首先由函数单调性定义,判断f(x)=x|x-a|在[2,+∞)上单调递增;然后把a分成a≤2与a>2两种情况分别进行检验,从而得出结论.
解答:∵函数f(x)=x|x-a|=
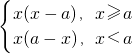 ,对于任意的x1,x2∈[2,+∞),x1≠x2,不等式
,对于任意的x1,x2∈[2,+∞),x1≠x2,不等式 >0恒成立,
>0恒成立,故函数在[2,+∞)上是增函数.
(1)当a≤2时,
若x∈[2,+∞),则f(x)=x(x-a)=x2-ax,其对称轴为x=
 ,此时
,此时 <2,所以,f(x)在[2,+∞)上是递增的.
<2,所以,f(x)在[2,+∞)上是递增的.(2)当a>2时,
①若x∈[a,+∞),则f(x)=x(x-a)=x2-ax,由于其对称轴为x=
 ,所以f(x)在[a,+∞)上是递增的;
,所以f(x)在[a,+∞)上是递增的;②若x∈[2,a),则f(x)=x(a-x)=-x2+ax,其对称轴为x=
 ,所以f(x)在[
,所以f(x)在[ ,a)上是递减的,
,a)上是递减的,因此f(x)在[2,a)上必有递减区间,故不满足条件.
综合(1)、(2)可知a≤2,
故答案为 (-∞,2].
点评:本题考查了函数单调性的定义,同时考查了分类讨论的思想方法,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|