题目内容
(本题满分18分,其中第1小题6分,第2小题6分,第3小题6分)
已知数列 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 当 时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
(3) 试判断:当 时,向量
时,向量
 是否可能恰为直线
是否可能恰为直线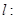
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.
【答案】
(1)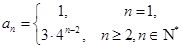 (2)
(2)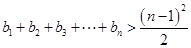
|
【解析】(1) 由
所以,数列 其中, 所以, (2)由题意, 当
所以, (3)由题意,直线 当 当
而此时等式左边的 解法二:同解法一,由假设可得 当 由 不妨设 |
故等式不可能成立. 所以,对任意的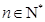 ,
,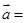
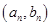 不可能是直线
不可能是直线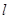 的方向向量.
的方向向量.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
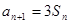 … (1) , 得
… (1) , 得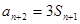 … (2),由 (2)-(1) 得
… (2),由 (2)-(1) 得 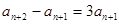 ,
整理得
,
整理得 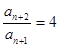 ,
,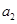 ,
,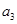 ,
, ,…,
,…, ,…是以4为公比的等比数列.
,…是以4为公比的等比数列.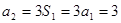 ,
,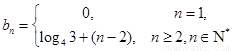 .
.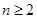 时,
时,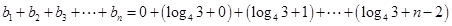
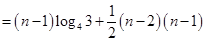
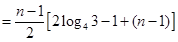
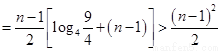
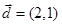 ,假设向量
,假设向量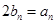 ,
,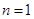 时,
时,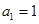 ,
,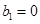 ,向量
,向量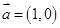 不符合条件;
不符合条件;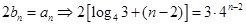
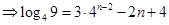 ,
,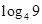 不是一个整数,而等式右边的
不是一个整数,而等式右边的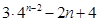 是一个整数,故等式不可能成立. 所以,对任意的
是一个整数,故等式不可能成立. 所以,对任意的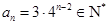
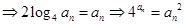 …①,
…①,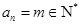 ,①即为
,①即为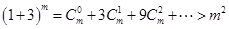
 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点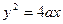 (
(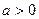 且
且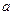 为常数),
为常数),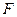 为其焦点.
为其焦点.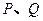 两点,且
两点,且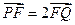 ,求直线
,求直线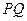 的斜率;
的斜率;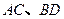 是过抛物线焦点
是过抛物线焦点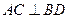 ,如图所示.求四边形
,如图所示.求四边形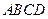 面积的最小值
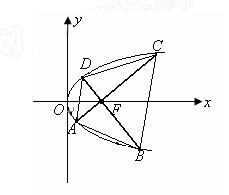
面积的最小值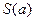 .
.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是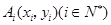 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
 准线上
准线上 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线 .
.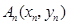 要么落在
要么落在 所表示的曲线上,
所表示的曲线上, 所表示的曲线上,并且
所表示的曲线上,并且 ,
, (不需证明);
(不需证明); 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求
 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
. 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; 上一点
上一点 经变换公式
经变换公式 与点
与点