题目内容
(本题满分18分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
(Ⅲ)过A、B分别作抛物C的切线 且
且 交于点M,求
交于点M,求 与
与 面积之和的最小值.
面积之和的最小值.

【答案】
解: (Ⅰ)设抛物线方程为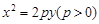 ,由题意得:
,由题意得:
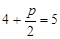 ,
,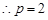 , 所以抛物线C的方程为
, 所以抛物线C的方程为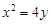 …4分
…4分
(Ⅱ) 解法一:抛物线焦点与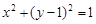 的圆心重合即为E(0,1),
的圆心重合即为E(0,1),
设过抛物线焦点的直线方程为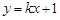 ,
,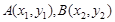 ,
,
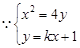 ,
,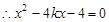 ,得到
,得到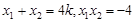 ,…2分
,…2分
由抛物线的定义可知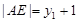 ,
,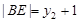 ,
,
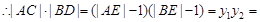
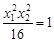 .即
.即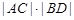 为定值1….3分
为定值1….3分
(Ⅲ)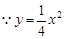 ,所以
,所以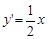 ,
,
所以切线AM的方程为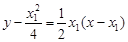 ,切线BM的方程为
,切线BM的方程为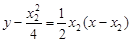 ,
,
解得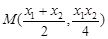 即
即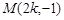 ……2分
……2分
所以点M到直线AB的距离为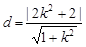 .
.
设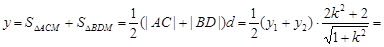
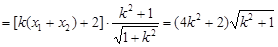 ….2分
….2分
令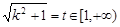 ,所以
,所以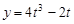 ,
,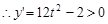 ,
,
所以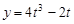 在
在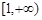 上是增函数,当
上是增函数,当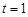 ,即
,即 时,
时,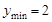 ,即
,即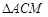 与
与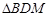 面积之和的最小值为2…3分
面积之和的最小值为2…3分
(Ⅱ)解法二:设过抛物线焦点的直线方程为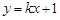 ,
,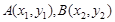 ,不妨设
,不妨设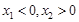 .
.
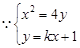 ,
,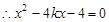 ,得到
,得到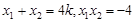 ,.2分
,.2分
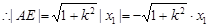 ,
, ,
,
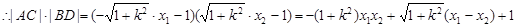
 ,即
,即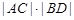 为定值….3分
为定值….3分
(Ⅲ)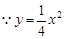 ,所以
,所以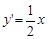 ,所以切线AM的方程为
,所以切线AM的方程为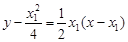 ,
,
切线BM的方程为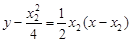 ,解得
,解得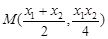 即
即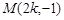 ……….3分
……….3分
所以点M到直线AB的距离为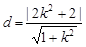 .
.
设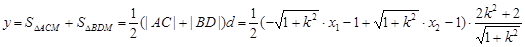
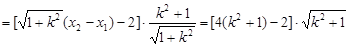 …3分
…3分
令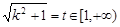 ,所以
,所以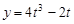 ,
,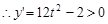 ,
,
所以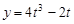 在
在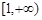 上是增函数,当
上是增函数,当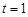 ,即
,即 时,
时,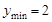 ,即
,即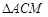 与
与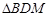 面积之和的最小值为2
面积之和的最小值为2
【解析】略

练习册系列答案
相关题目